Discrete event traffic simulation, laggy heads, and ghosts

By Dustin Carlino, last updated September 2021

A/B Street's traffic simulation isn't based on any research papers or existing systems, so this article aims to motivate and explain how it works. This article focuses on how the different agents (drivers, bicyclists, and pedestrians) move around. If you're wondering how we figure out where these agents should go or what time they decide to take trips, go read about travel demand models.

I'm not aiming to survey how other traffic simulation models work here. In short, some focus on "macroscopic" patterns, like the volume of traffic along a particular highway over time. A/B Street is more on the "microscopic" side, modeling individual agents making decisions over time. Many such models use "discrete-time" simulation, where every agent senses and reacts to the world every time-step (0.1 seconds or so). A/B Street actually started with this -- see the appendix for more background. But early on, I switched to a discrete-event simulation instead. So, let's jump into that!

Note: I'll provide references to the current implementation. Someday I'll write that article describing how to build a traffic simulation from scratch...

• Starting simple: Pedestrians
  • Discrete events
• Vehicles
  • The state machine
  • Exact positions
  • Laggy heads
  • Performance
• Lane-changing
  • Background
  • Step 1: deciding to change lanes
  • Step 2: performing the lane-changing
  • Future work
• Appendix: discrete-time simulation

Starting simple: Pedestrians

Imagine a simple movement model for pedestrians. Usually they exist at some point along a sidewalk and can move in one direction or the other. At intersections, different sidewalks are connected by crosswalks, and pedestrians can also move bidirectionally on those, after waiting for the right time to cross.

We'll make a few assumptions about pedestrians. They follow the sidewalks and crosswalks perfectly, never deciding to honor their inner Pythagorean. They travel at a fixed speed and change that speed instantly -- no smooth acceleration. That fixed speed could depend on both their preferred walking speed and on the current sidewalk's elevation gain. These poor robotic pedestrians never stop to smell the flowers, write an angry neighborly note, or pet a pupper -- they just walk, or wait. Online dating is also so pervasive in this simulation that pedestrians ghost -- through each other, that is. There are more interesting models of pedestrian movement like the social force model where people change speeds in crowds, but A/B Street is focused on sad American cities where you don't often see many people walking in one place. So there's no collision between pedestrians at all; they just pass through each other, temporarily losing their individuality for rendering purposes:

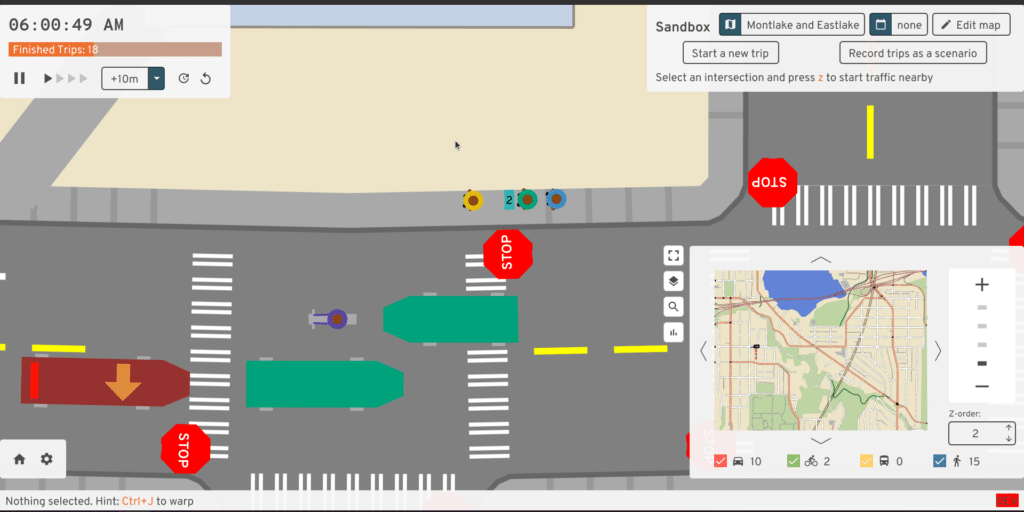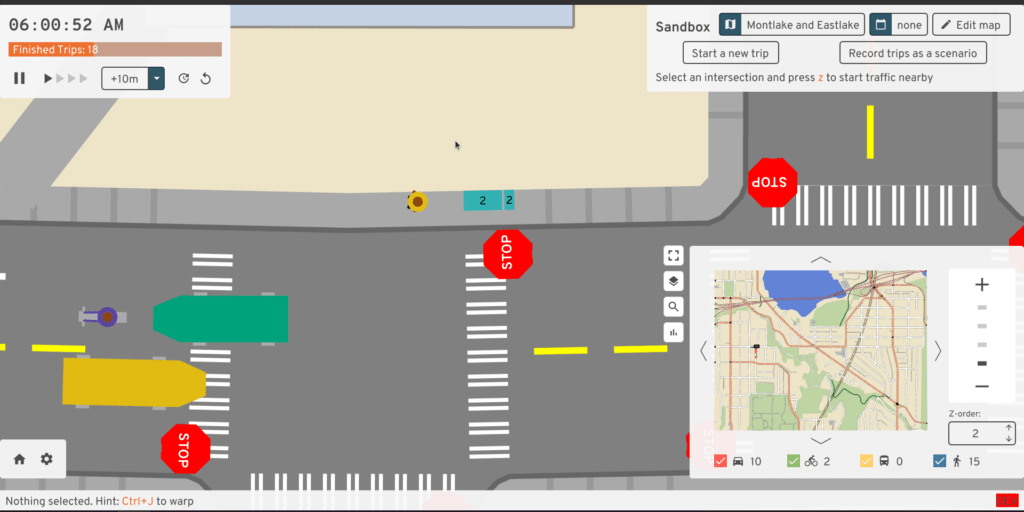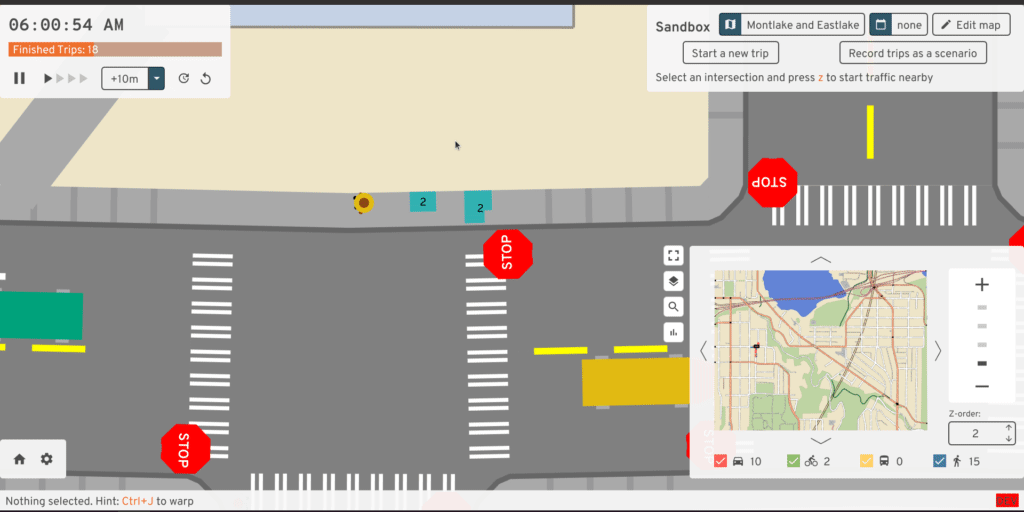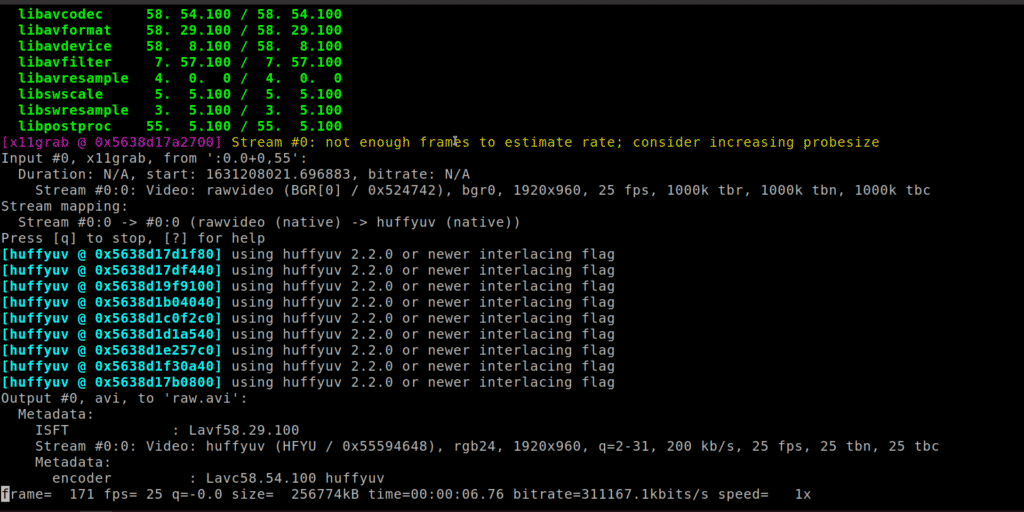
In the world of discrete timesteps, you could imagine each pedestrian has very simple logic. At any moment, they just continue walking one direction or the other at their fixed speed along a sidewalk or crosswalk. Or they pause at the end of a sidewalk, awaiting their turn at a stop sign or traffic signal.

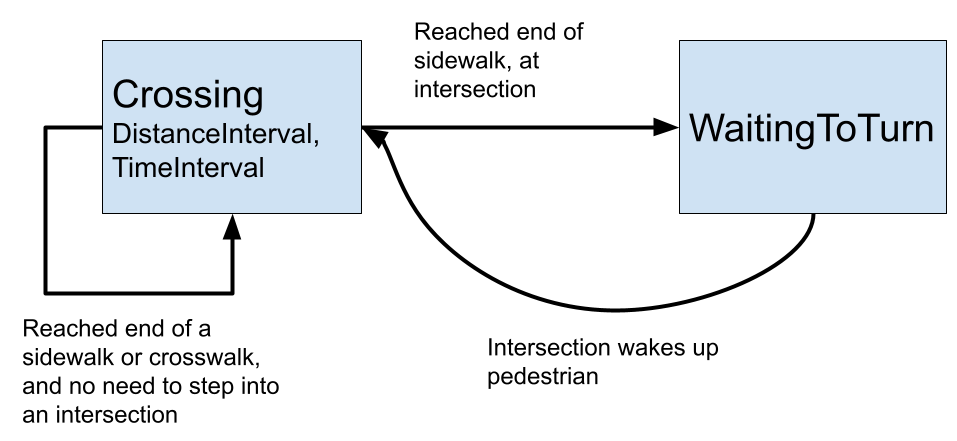
Discrete events

Don't the constant updates every time-step seem wasteful? Most of the time, a pedestrian is in a steady-state -- walking or waiting. Since they walk at a fixed speed, we can just linearly interpolate their exact position at any moment in time if we want to draw them.

Instead of looping through every agent every time-step, in a discrete-event system, we just have one giant priority queue of events, scheduled to happen at some time in the future. Each agent remains in a certain state for a period of time, and schedules an event to transition themselves to a different state.

In the case of pedestrians, this works like this:

1. A pedestrian begins at 30 meters distance along their first sidewalk. They want to walk forwards on the sidewalk, so they calculate the distance to the end of the sidewalk -- say another 70 meters -- and divide that by their preferred speed, scheduling an event an appropriate amount of time later -- say 10 seconds.
2. For the next 10 seconds, that pedestrian is in the Crossing state, which has a DistanceInterval stating that they're moving on a certain sidewalk from 30 to 70 meters. The TimeInterval says that this state is occurring from time 0 to 10 seconds. We can linearly interpolate to find their position for drawing.
3. At 10 seconds, the scheduler wakes up the pedestrian. They're now at the end of the sidewalk, so they look at the intersection and ask to cross. There's a traffic signal, and the almighty hand says NOPE, so they hand over control to the intersection and just mark themselves as WaitingToTurn state. No events are scheduled to update them.
4. But the intersection remembers the list of waiting agents. Some time later, the light changes, and the intersection "wakes up" all of the agents who now have a green.
5. Our pedestrian calculates a new Crossing state for the crosswalk. This state too happens over some distance and time interval.
6. At the end of the crosswalk, the pedestrian immediately enters another Crossing state for the next sidewalk.

We can visualize this with a finite-state machine:

Code references here.

Vehicles

Discrete events are obviously much simpler for pedestrians, but there were some pretty drastic assumptions there that won't work for vehicles. It takes a few more tricks for A/B Street to model cars, bikes, and buses (I'll just use "vehicle" from here on.)

First let's understand what vehicles can do. They travel in one direction along individual lanes, and they queue behind each other -- no ghosting. At intersections, they wait as needed, then move along a "turn," destined for a target lane. There are two major differences from reality that we'll take as assumptions.

First, vehicles instantly change speeds -- no smooth acceleration from rest, or modeling of safe stopping distance. So if a vehicle starts at the beginning of an empty lane, they instantly jump from rest to the maximum speed limit for that road. They travel at that maximum speed limit until the moment their front bumper strikes the boundary between road and intersection, then they stop immediately. This doesn't model highway driving at all, where things like jam waves are interesting to study and require more realistic kinematics and a model of driver reaction time. But A/B Street is focused on in-city movement, and the essence of scarcity I want to model is capacity on lanes and contention at intersections. What happens in between isn't as important. I think you'll find that the overall traffic patterns emerging in A/B Street still look compellingly realistic.

The second article of funny business is lane-changing. Let's assume that vehicles don't change lanes in the middle of a road. Instead, vehicles shift left and right while moving through intersections. So if somebody needs to use a left turn lane, then at the intersection one road back, they'll choose to slide over during their turn. Any conflicting movements with other vehicles is handled at the intersection already.

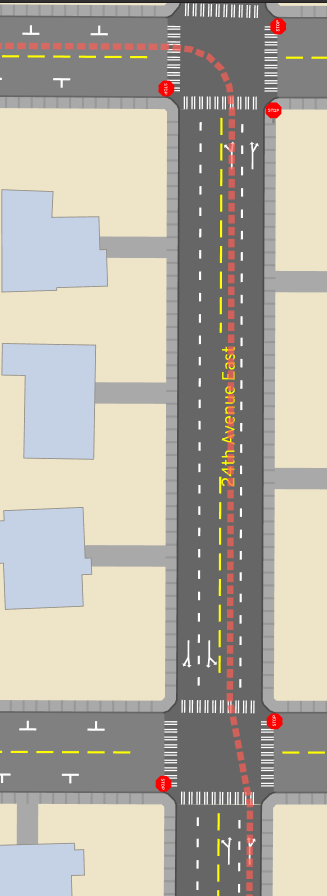
This also means there's no over-taking. If a car gets stuck behind a bike moving slowly uphill, so be it.

We'll try to relax this second assumption later.

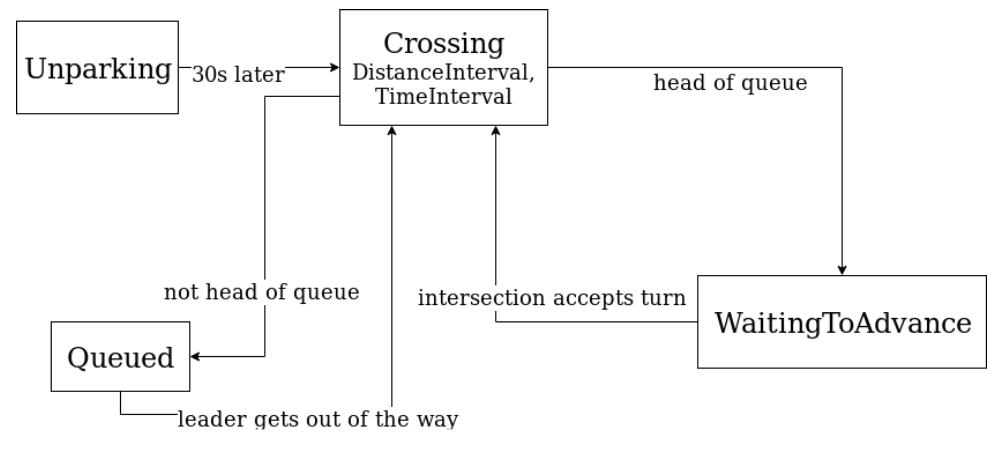
The state machine

So let's figure out how to model these vehicles. The approach used by pedestrians, with Crossing and WaitingToAdvance states doesn't quite work, because nothing would stop vehicles from plowing into each other. So let's introduce a third state -- Queued. When a vehicle enters a new lane, it enters the Crossing state as usual, calculating the "best-case" time to cross the entire length of the lane at the max speed limit. This assumes nobody's in the way! But when this state ends, we can only transition the vehicle to the WaitingToAdvance state if they're the "lead" vehicle in the current lane's queue. If they have a "leader" vehicle, then they enter the Queued state and register as a "follower" of this "leader" in the queue.

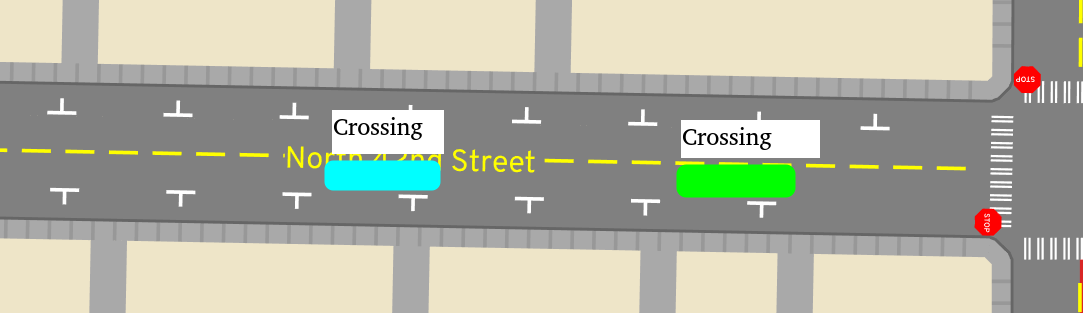
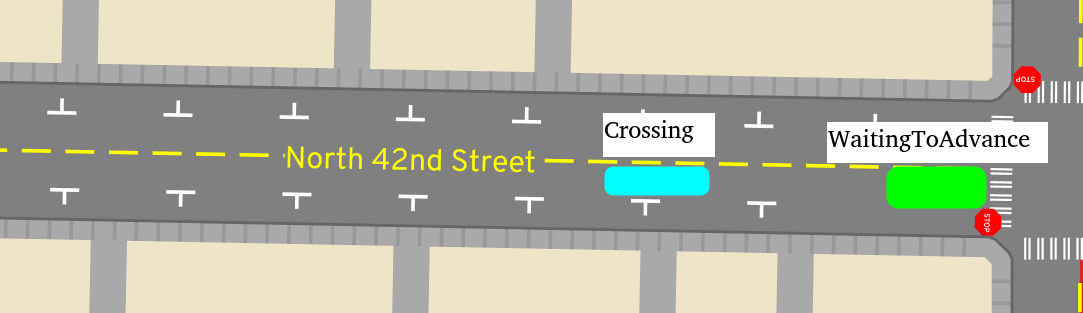
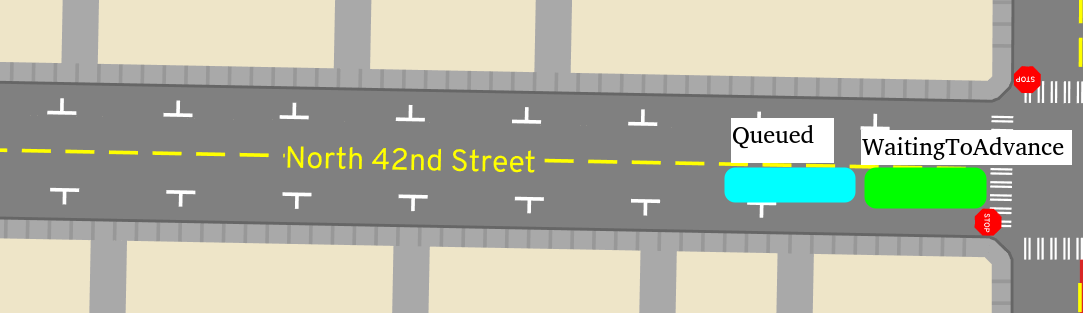
Note that somebody might enter Queued well before they're near the intersection, like if they're following a slower vehicle. Queued just means the faster vehicle has already spent the "best-case" time to cross the road at the full speed limit.

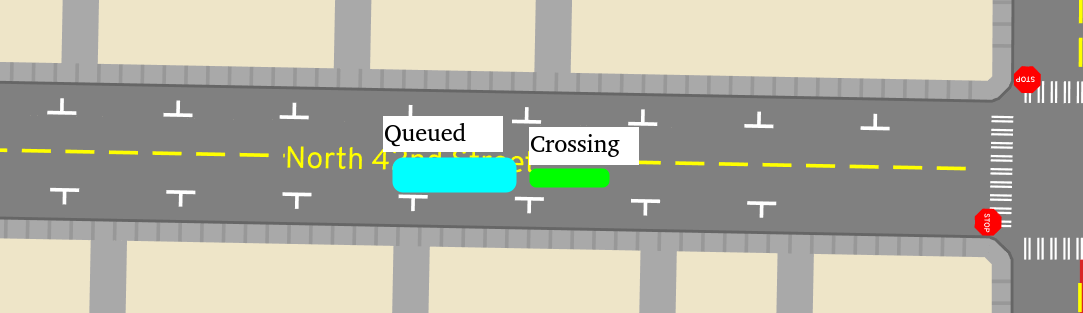
When the vehicle at the very front of a lane enters the intersection and fully vacates their old lane, then they "wake up" their follower. Since the Queued follower has been following along as closely as possible, they instantly transition to WaitingToAdvance, since we know they're at the end of the lane. "Fully vacating" the lane means the back of the vehicle clears the lane; see the section below.

We can again understand all of this with a finite-state machine:

Code references here and here.

Exact positions

Most of the time, we don't care exactly where on a lane some vehicle is. But we do need to know for drawing and for a few cases during simulation, such as determining when a bus is lined up with a bus stop in the middle of a lane.

To calculate exact positions, we walk along each lane's queue from front to back. The key idea is that leaders bound the position of followers, and we can "lazily evaluate" the position of followers. This means that calculating one vehicle's position costs as much as calculating the entire queue's in the worst case, but that's usually fine -- for drawing, we want everyone anyway.

The process is simple. We use each vehicle's state to determine the "best-case" position of their front bumper. WaitingToAdvance means the vehicle is at the very end of the lane. For vehicles still Crossing, we linearly interpolate the time and distance intervals. Then as we walk from front to back, we maintain a "bound" for the next vehicle's position. This is based on the front position of the current vehicle, plus the vehicle's length and a fixed following distance (which, note, is not based on speed).

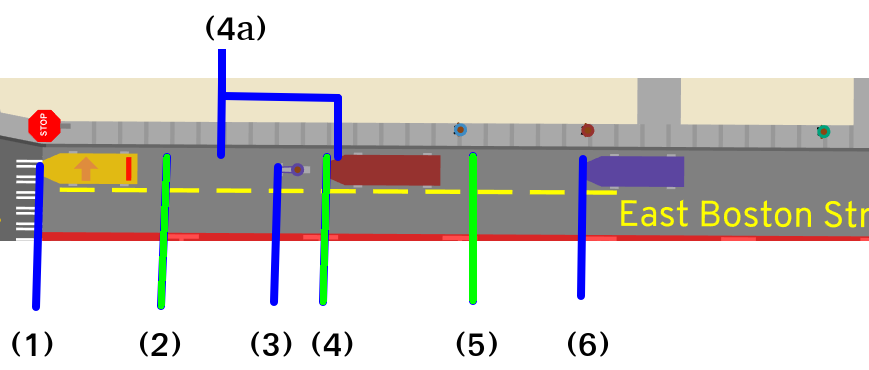
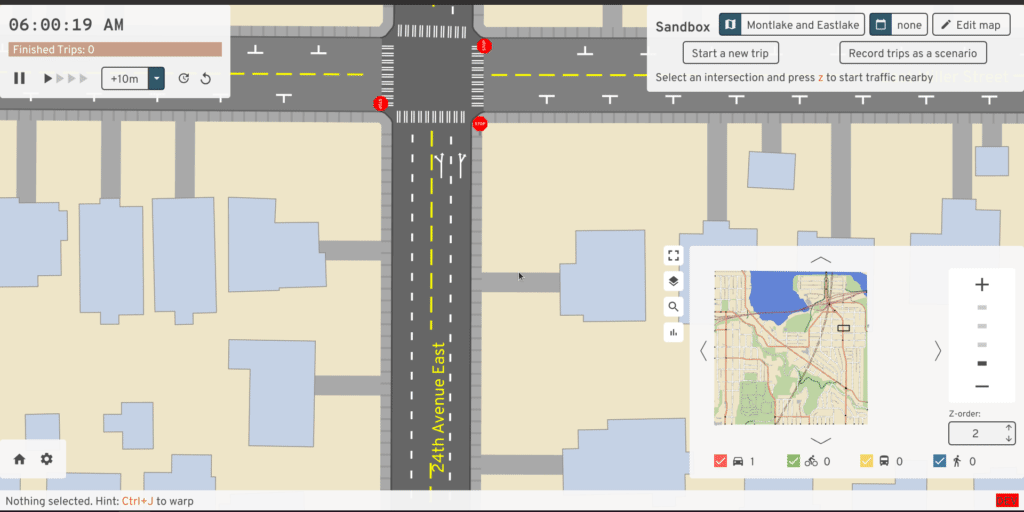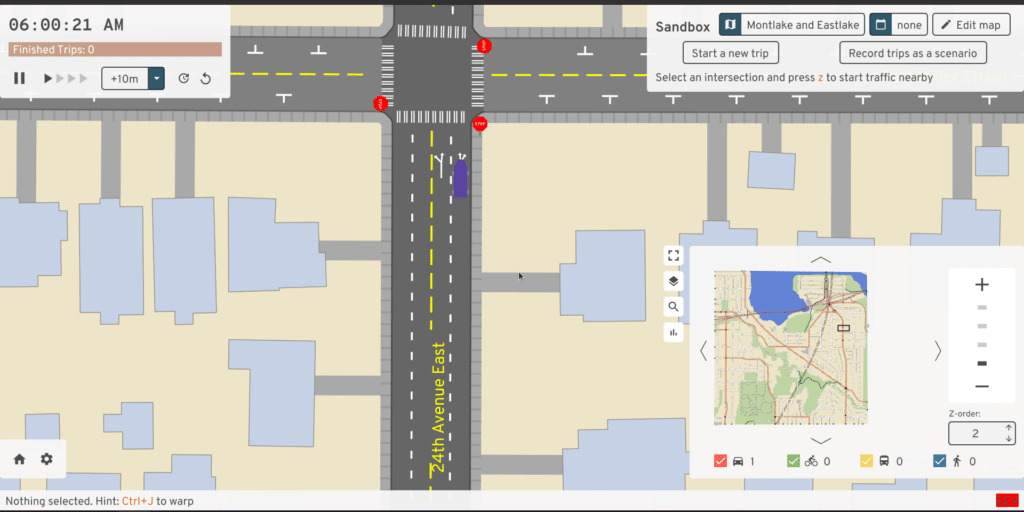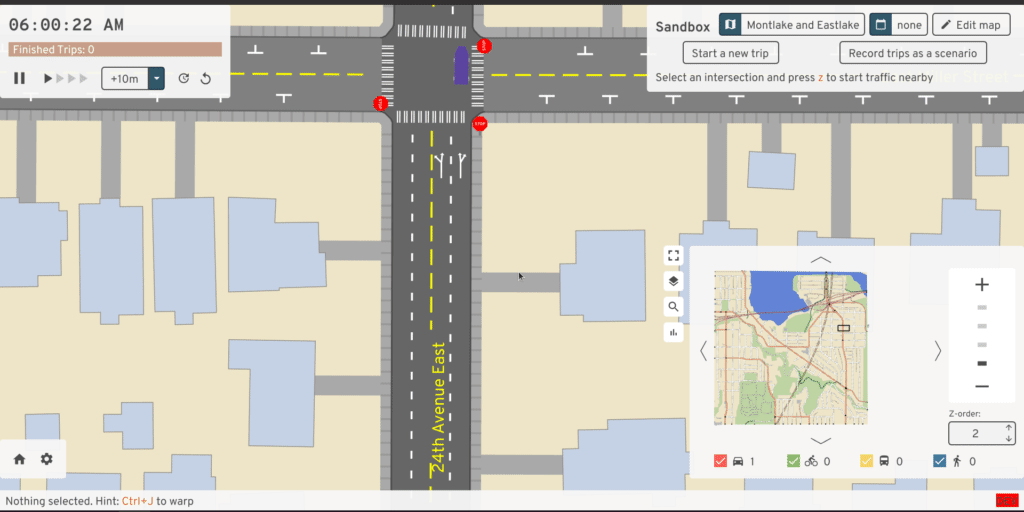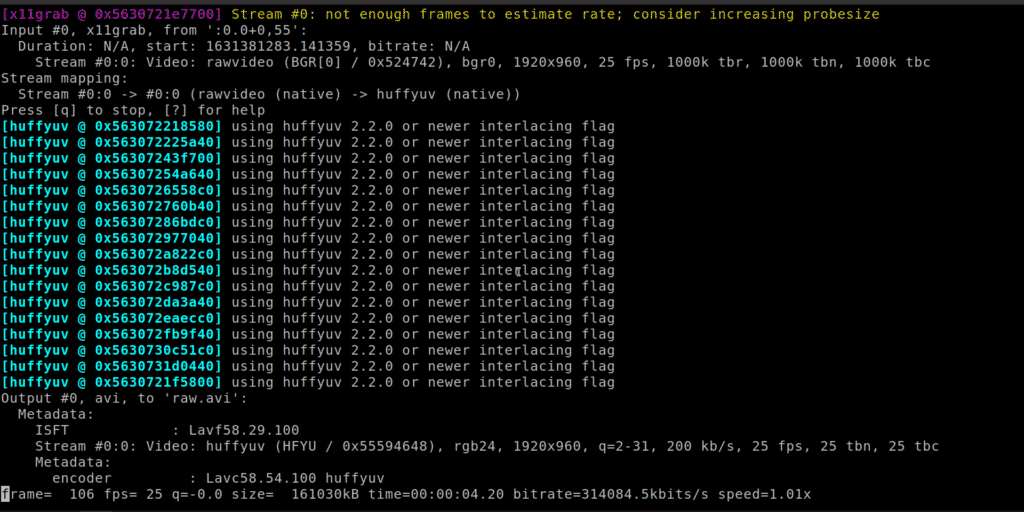
Let's walk through the example above, from front (the left side) to back. The yellow car is WaitingToAdvance at the intersection, so their front position (1) is the full length of the lane. Based on the length of that car and a following distance of 1 meter, the bound imposed by this first car is at (2) -- nobody following could possibly be beyond this position.

The second vehicle in the queue is the bike. Based on their Crossing state, which says they're crossing from 0 meters along the lane to the full length of it from 30 seconds to 90 seconds, we linearly interpolate and get their front position (3). This position is smaller than the bound of (2), so no adjustment is needed.

The third vehicle is the red car. Based on their Crossing state, optimistically they would be at position (4a) by this time. But since they're following the bike, then they're bound by position (4), so that's where this algorithm places them. The bound for the next vehicle is then (4) plus the vehicle's length and a following buffer, giving us (5). The final vehicle hasn't reached that position yet based on its Crossing state, so it's unaffected by that bound and is just at (6).

Code here.

Laggy heads

Vehicles aren't infinitesimal dots; they have a length, so each one has a front and back. This means we have to be a little careful about defining when a vehicle has left a lane and its follower should be considered the "first" in the queue:

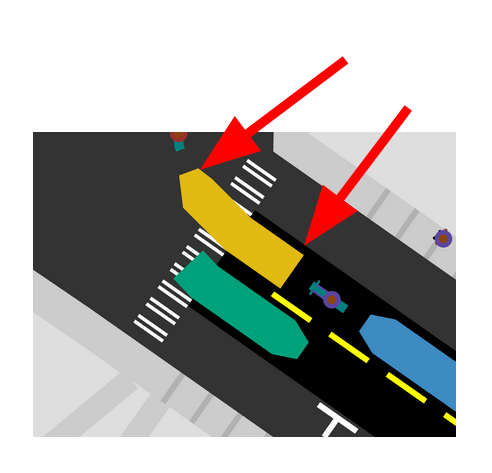
To model this, every lane's queue may have a "laggy head." (Naming things is hard...) The head of this queue may be the bike, but because the yellow car is still the laggy head, the bike remains Queued. When the yellow car enters the intersection, we need to determine when its back will clear the lane, letting the bike wind up at the very front. Optimistically we assume the yellow car will travel through the turn as fast as possible, so we can calculate the time to cross the car's length, and schedule a check there. When that check happens, we calculate the exact position of the yellow car -- maybe it's queued behind other vehicles making the same turn, or blocked by other vehicles in its target queue. If it's advanced far enough, then we unregister the yellow car as a laggy head and wake up the bike, who changes from Queued to WaitingToAdvance. If the yellow car's back end is still sticking out into the lane, then we schedule another check a fixed 0.1 seconds. This retry policy is quite aggressive and will slow down the simulation as traffic jams start to form.

This logic to determine when a vehicle's back has fully cleared a lane is unfortunately complicated by the presence of short roads and turns, a currently unsolved problem in the underlying map model. A long vehicle like a bus may partly be overlapping several lanes and turns at a time, meaning we have to carefully calculate when the back of the bus has cleared each piece.

Performance

It's been a very long time since I've measured the performance of this discrete-event simulation, so these numbers are rather out-of-date:

One of the reasons the simulation is more performant than discrete time-steps is by how much time the simulation advances between updates. With discrete time, it's always a fixed amount -- 0.1 seconds usually. With discrete events, it depends when the next event is scheduled -- the later that event occurs, the faster the overall simulation proceeds. On a nearly empty map with really long roads, a single agent only needs a few updates to complete its trip -- very loosely, an update at the beginning and end of each lane and turn in its path. As more vehicles queue along the same lane at the same time, we increase the number of updates to process all of them, but it's still less than updating every agent every 0.1 seconds.

There are a few big opportunities to improve performance, by requiring less updates when vehicles are stuck waiting at intersections or stuck behind laggy heads. From some older investigation, it's clear that a huge amount of processing is spent on agents trying to start a turn and on checks that a laggy head has cleared a queue.

Lane-changing

For a long time, A/B Street had no dynamic lane-changing or over-taking. As described earlier, vehicles use the conflict handling at intersections to change lanes in order to pick the lane required for a turn ("mandatory lane-changing") or that's likely to be fastest ("discretionary lane-changing"). But that finally changed in June 2021.

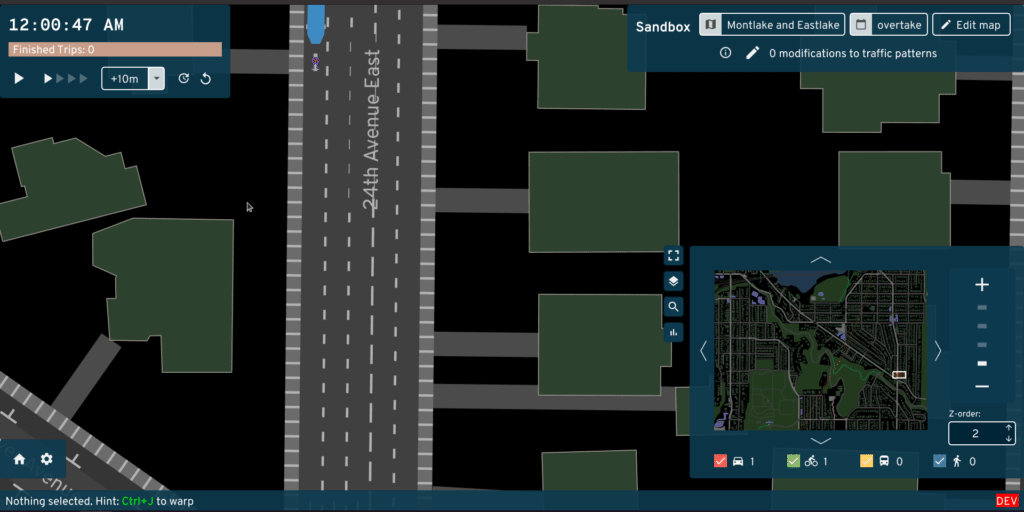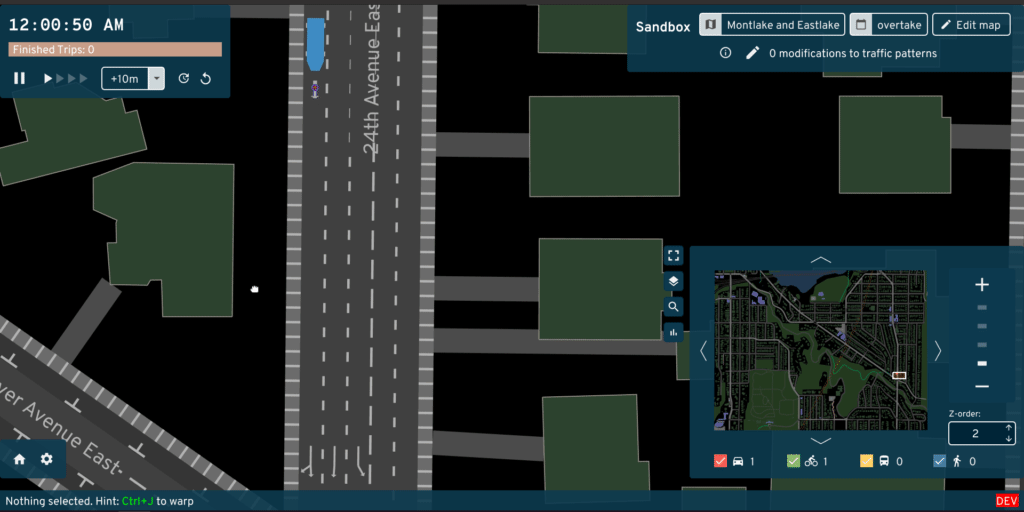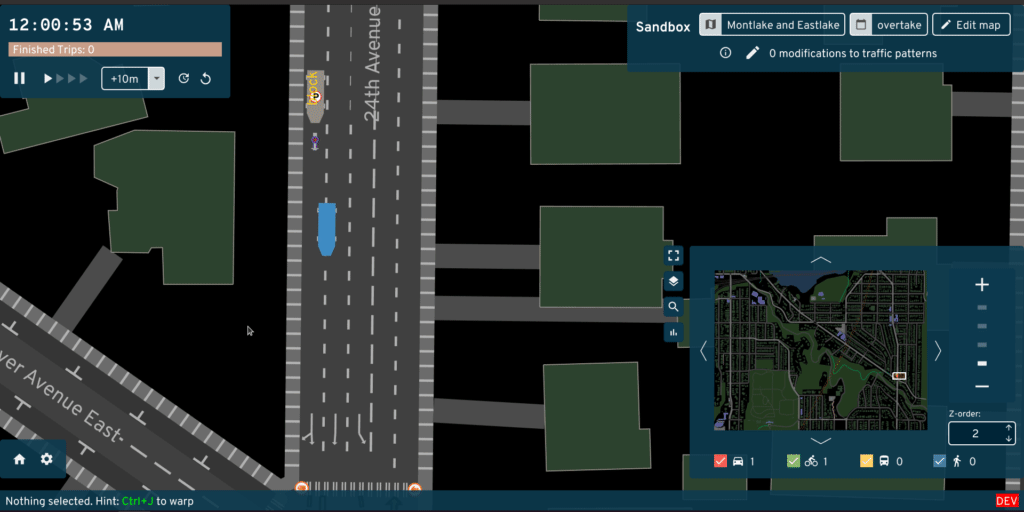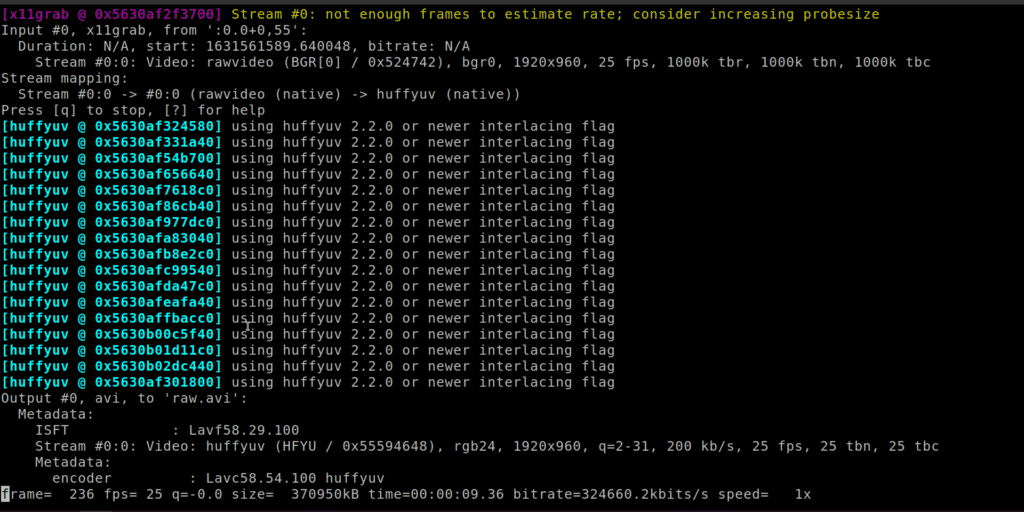
Background

The lane-changing implemented right now is only discretionary, meant for cars to over-take slower vehicles. In a previous project, I tried implementing mandatory lane-changing. But the process could fail -- if there wasn't room for a vehicle to start changing lanes, it would just continue on the current lane and miss the turn it was supposed to take. That forced rerouting. Since the lane-changing process is scoped to happen on a single road -- which seems pretty necessary to manage complexity, and also prevent changing lanes in the middle of an intersection -- this meant that clusters of short roads in the map model really caused major problems. Many vehicles repeatedly attempted lane-changing maneuvers required by pathfinding, but impossible to actually pull off in the simulation. This greatly skewed results -- some agents experienced really high trip times as they repeatedly rerouted and kept attempting difficult maneuvers.

I considered making the process infallible -- vehicles would slow down and eventually stop, until they forced their way into another lane. I suspect this could also lead to lots of unrealistic gridlock, but I never tried it.

So that's why there's only discretionary or "opportunistic" lane-changing for now.

Step 1: deciding to change lanes

The current implementation will now be described. The process starts when a vehicle transitions from Crossing to Queued. The follower will compare its ideal speed to that of its leader. If the leader is still Crossing and has a slower speed, then the follower will try to over-take. If the leader is also Queued, then there's probably no opportunity to over-take -- the follower is probably just hitting the end of a chain of vehicles waiting for an intersection.

Next the vehicle will pick a lane to use for over-taking. There's currently no support for crossing a road's center line and temporarily using a lane in the opposite direction. The target lane must also be compatible with the vehicle's path, so if there's a turn coming up, nothing will happen.

Finally, the vehicle will attempt to initiate the lane-changing. There's a bunch of checks in the code that I won't repeat here. In summary, we require a fixed 1 second duration to perform the manuever. During this, the vehicle will exist in two queues. Committing to the move requires completion before reaching the end of the road, and nothing in the way in the target lane.

Step 2: performing the lane-changing

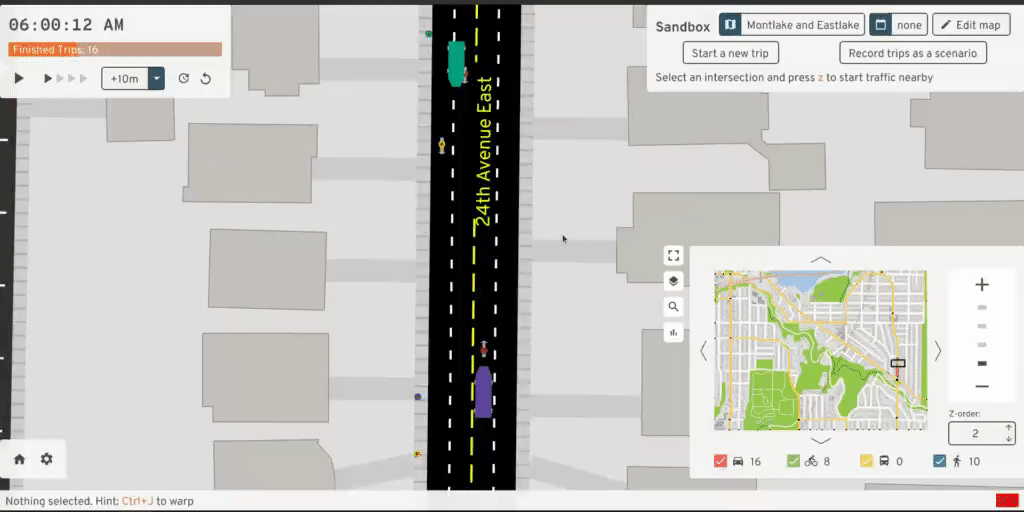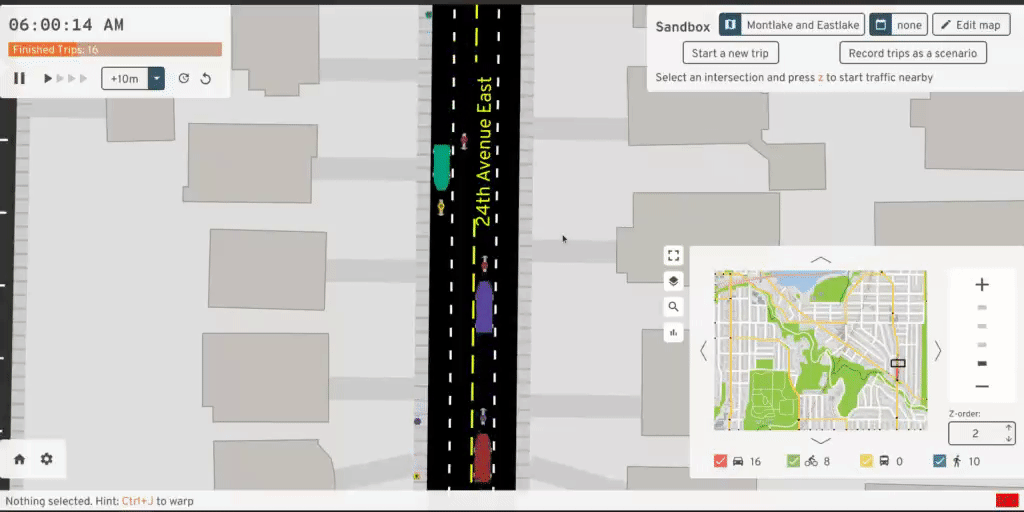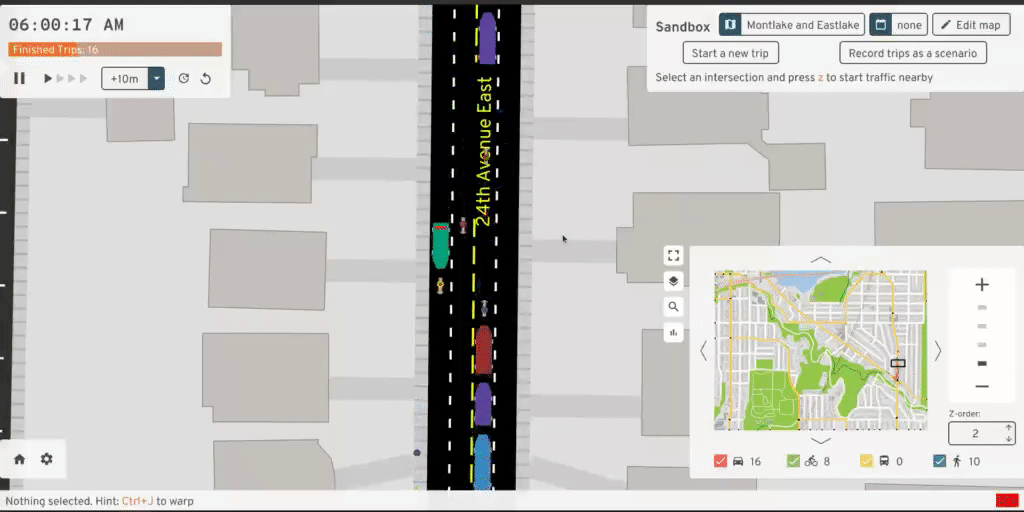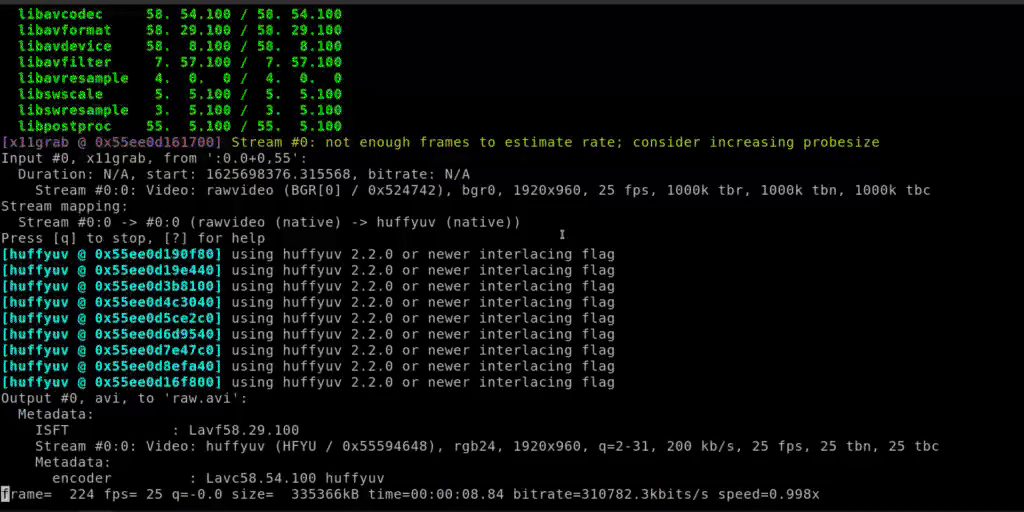
The vehicle enters the ChangingLanes state, which works almost exactly like Crossing. The vehicle immediately "warps" to their target lane. They exit their original lane, replacing themselves with a "ghost" in that queue. The ghost follows the leader vehicle and shares the same length as the actual vehicle. This ghost prevents another vehicle from advancing too close to the slow leader and "clipping" into the vehicle changing lanes.

Future work

There are many limits with the current approach.

First, vehicles should be able to change lanes twice and return to the original lane, actually passing a slower vehicle. I got a proof-of-concept working. The idea is to "acquire a lock" on both lane-changing movements at the same time, so that a vehicle doesn't start to over-take and then wind up unable to return to the original lane. This involves inserting a ghost in front of the slow vehicle, but there are some unsolved conceptual problems that I've... completely lost context on.

Once full over-taking works, letting vehicles cross into incoming traffic to over-take would be the next step. This will require calculating what part of that opposite direction queue should be blocked off for the duration of the movement.

There are some smaller things to polish:

• A lane-changing vehicle can visually "clip" into the slow leader, due to the vehicle's front position no longer being bound by the slow leader. See here for a bit of detail.
• Start the first step before a vehicle enters Queued. This is the reason why cars will follow a bike for a few seconds before trying to pass. This could be done by calculating the time at which a faster follower will intersect a slower leader, and scheduling an event to possibly initiate lane-changing then.
• Once a vehicle decides it wants to pass somebody, it only checks if there's room in the target lane once. If there happens to be somebody in the way, it gives up. We could schedule more retries, possibly based on how busy the target lane is. But if this is too aggressive, at some point we degrade to the performance of time-steps.

Appendix: discrete-time simulation

A/B Street's first traffic model was discrete-time, meaning that every agent reacted to the world every 0.1s. Cars had a more realistic kinematics model, accelerating to change speed and gradually come to a halt. Cars did a worst-case estimation of how far ahead they need to lookahead in order to satisfy different constraints:

• Don't exceed any speed limits
• Don't hit the lead vehicle (which might suddenly slam on its brakes)
• Stop at the end of a lane, unless the intersection says to go

After fighting with this approach for a long time, I eventually scrapped it in favor of the simpler discrete-event model because:

• It's fundamentally slow; there's lots of busy work where cars in freeflow with nothing blocking them or stopped in a long queue constantly check to see if anything has changed.
• Figuring out the acceleration to apply for the next 0.1s in order to satisfy all of the constraints is really complicated. Floating point inaccuracies cause ugly edge cases with speeds that wind up slightly negative and with cars coming to a complete stop slightly past the end of a lane. I wound up storing the "intent" of an action to auto-correct these errors.
• The realism of having cars accelerate smoothly didn't add value to the core idea in A/B Street, which is to model points of contention like parking capacity and intersections. (This is the same reason why I don't model bike racks for parking bikes -- in Seattle, it's never hard to find something to lock to -- this would be very different if Copenhagen was the target.) Additionally, the kinematics model made silly assumptions about driving anyway -- cars would smash on their accelerators and brakes as hard as possible within all of the constraints.

And if you made it this far, have a poem about discrete event simulation (and also compilers) that I wrote many years ago...