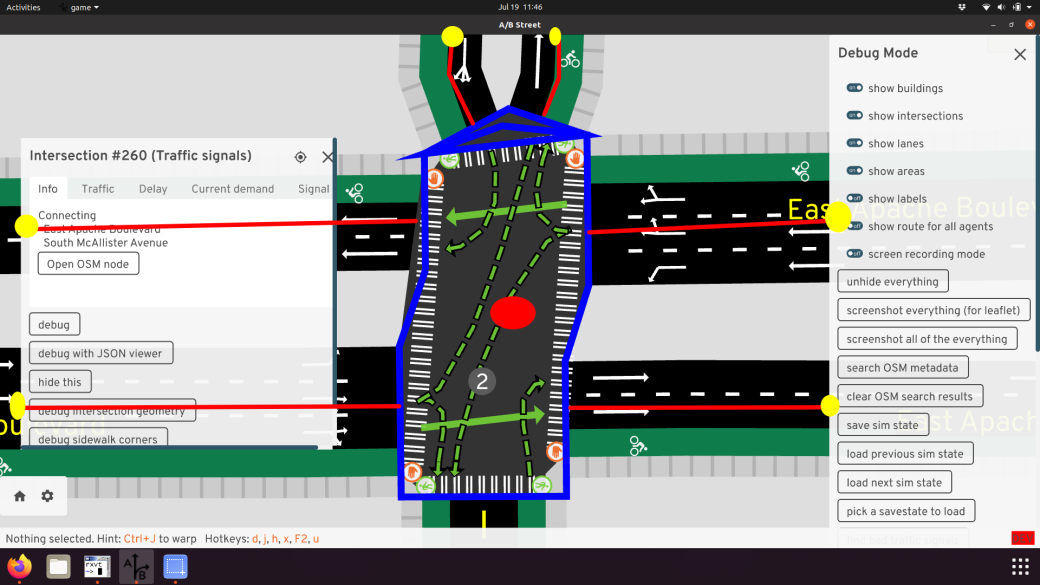
Deep dive into devilish details: Intersection geometry
By Dustin Carlino, last updated September 2021
Some of the things in A/B Street that seem the simplest have taken tremendous effort. Determining the shape of roads and intersections is one of those problems, so this article is a deep-dive into how it works and why it's so hard.
Note: The approach I'll describe has many flaws -- I'm not claiming this is a good solution, just the one that A/B Street uses. If you see a way to improve anything here, let me know about it!
- Trying this out
- Background
- The main process
- Interlude: problems so far
- Intersection consolidation
- Conclusion
- Appendices
Trying this out
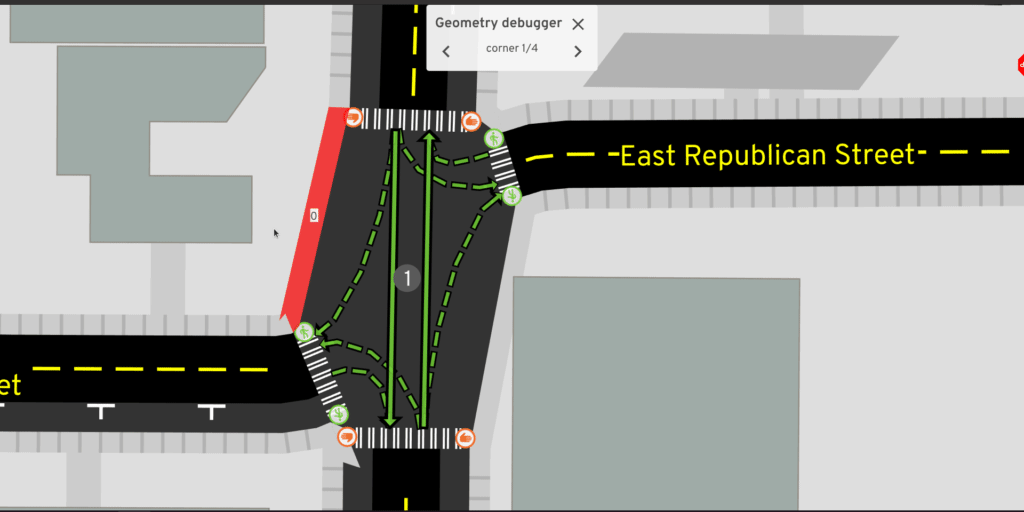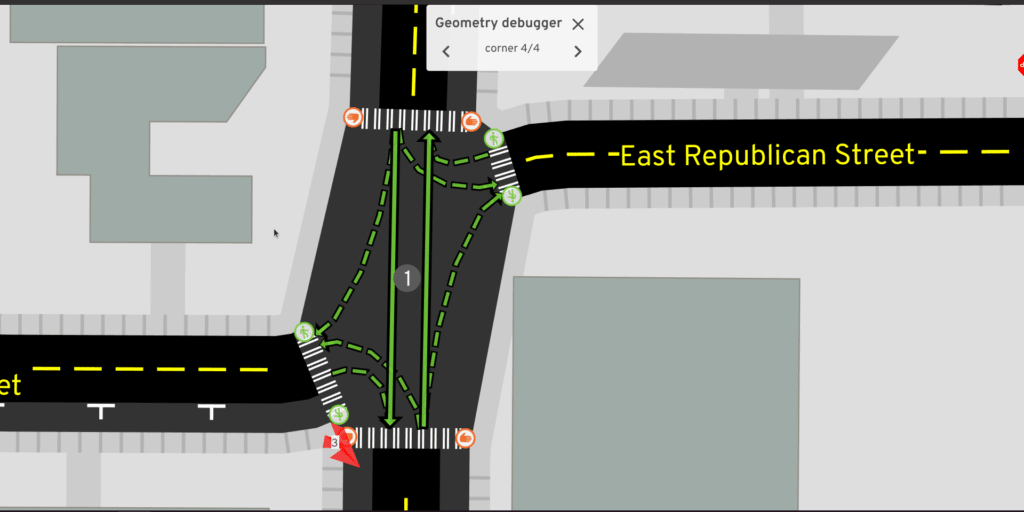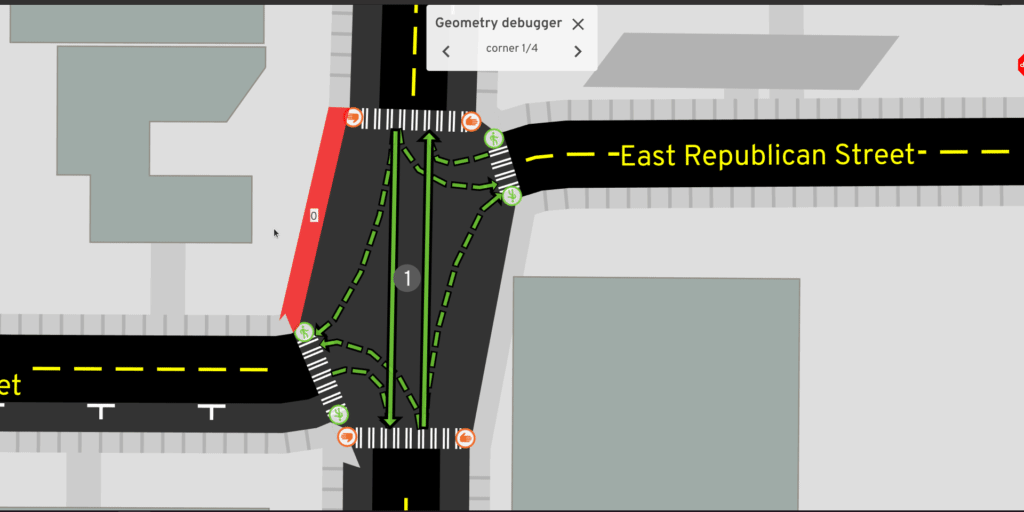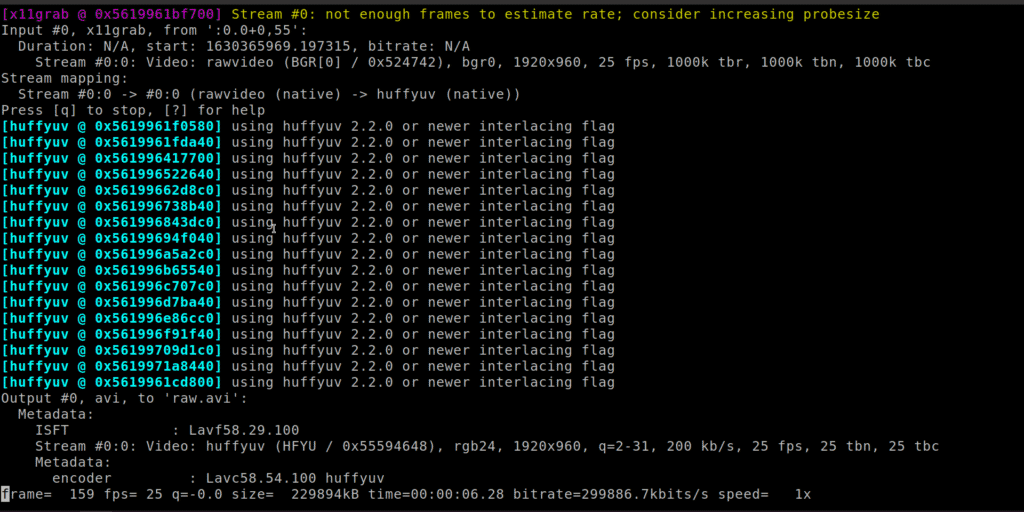
Originally I wanted to embed code in this article and have interactive demos to explore each step. That level of ambition fell through, but there is a geometry debugging tool, running in your browser (with WASM and WebGL required): launch the tool.
The tool wasn't designed for ease-of-use, so some hints on using it:
- Click and drag to move, scroll to zoom
- Toggle intersection geometry on/off with the right panel or by pressing g
- Click and drag an intersection or an internal point in a curved road to move it
Background
Most street maps you'll find provide a simplified view of streets. Google Maps, Apple Maps, and most OpenStreetMap (OSM) renderers mostly just tell you the road's name, color it by type (a highway, major arterial road, minor residential street), take great liberties with the width, and don't explicitly distinguish intersections from roads. These maps are used for navigation and drawing your attention to nearby businesses, so this is quite a reasonable view.
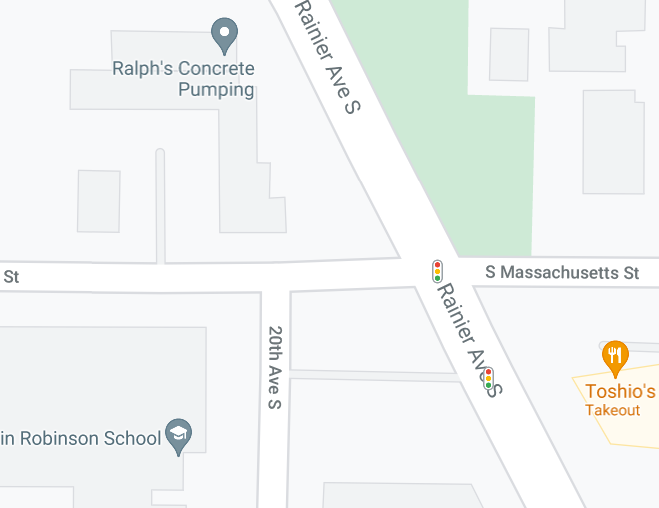
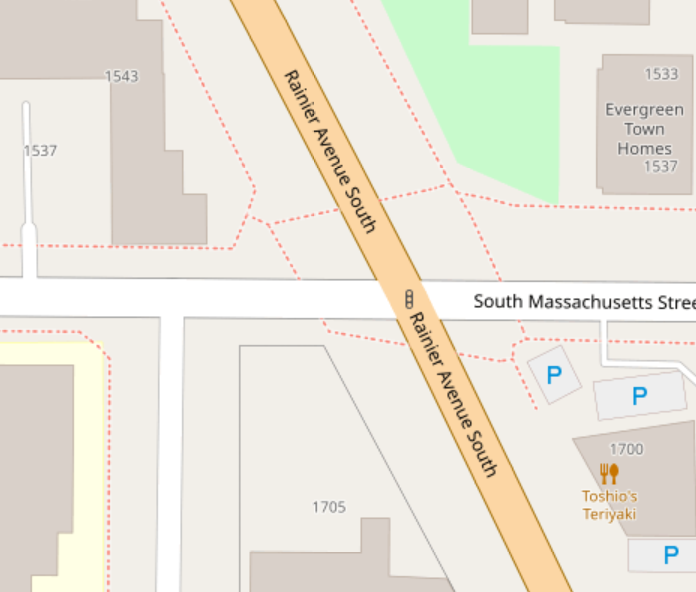
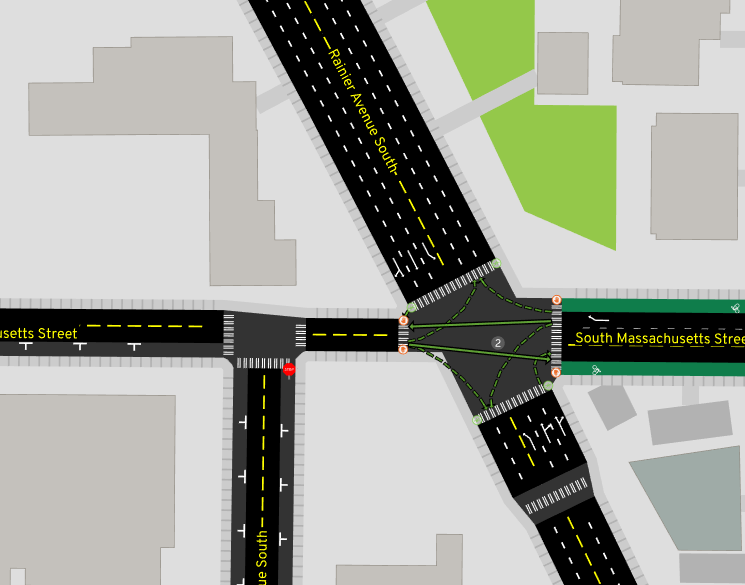
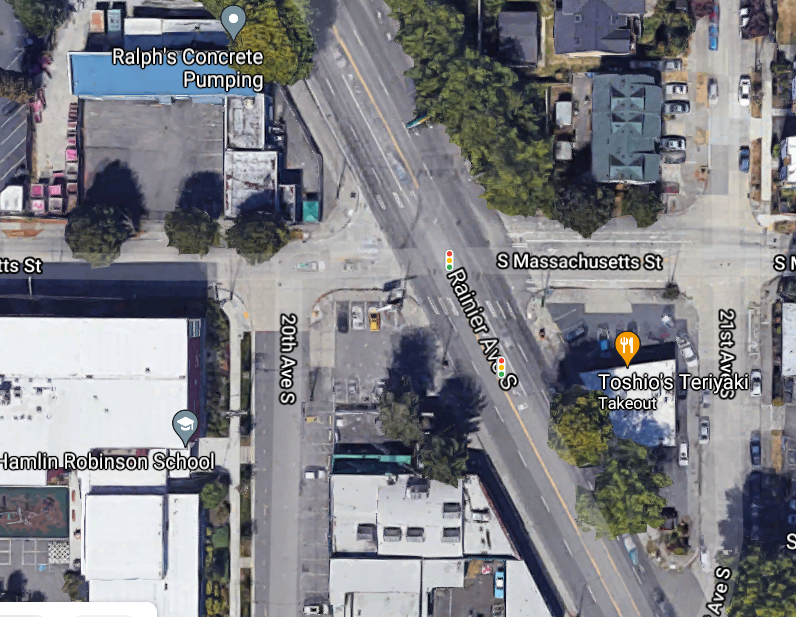
A/B Street is all about imagining how traffic moves through a city and exploring the effects of redesigning streets. So of course, we need way more detail. To imagine a bike lane down Eastlake Ave instead of street parking, we need to first see how the street's space is allocated. To propose a more pedestrian-friendly traffic signal crossing from Husky Stadium to the UW medical building, we need to see that huge intersection.
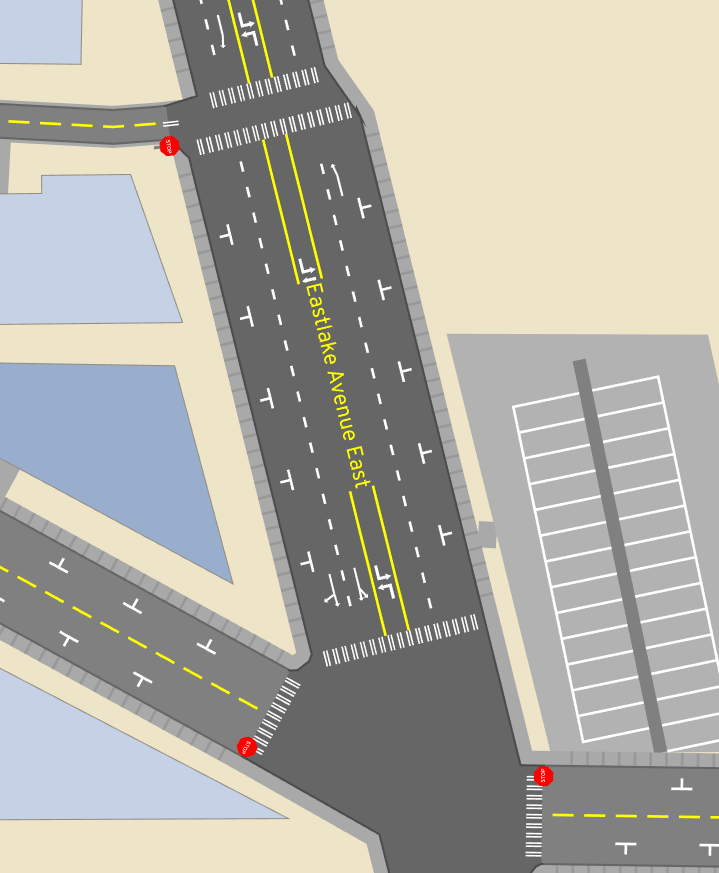
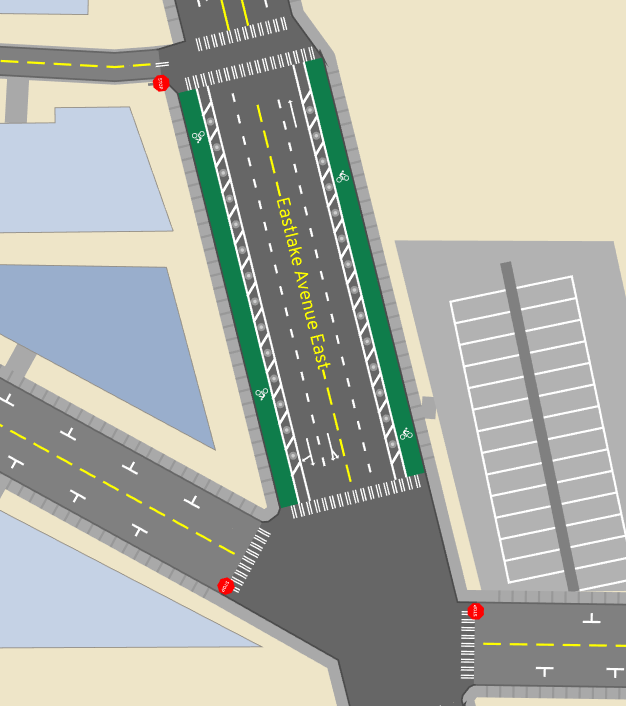
At a high-level, we want a representation that:
- Clearly communicates how a road is divided into different types of lanes (general purpose driving, turn lanes, bike lanes, bus-only lanes, street parking, sidewalks)
- Represents the total road width, which tells us how we might change that lane configuration
- Divides paved area into distinct roads and intersections. This division tells us where vehicles stop before entering an intersection, how pedestrians and vehicles are likely to move through the space, and what conflicts between them might occur.
We're constrained to publicly available, free data sources. Although some cities have GIS departments with some datasets that might be helpful, we're pretty much going with OpenStreetMap (OSM), which has decent coverage of most cities worldwide.
Desired output
Let's be a little more specific about the representation we want. If you imagine a city as flat 2D space, roads and intersections occupy some portion of it. (Let's ignore bridges and tunnels.)

We want to partition this space into individual intersections and road segments. Each road segment (just called "road" for simplicity) leads between exactly two of those intersections. This partition shouldn't have any ambiguous overlap between objects.
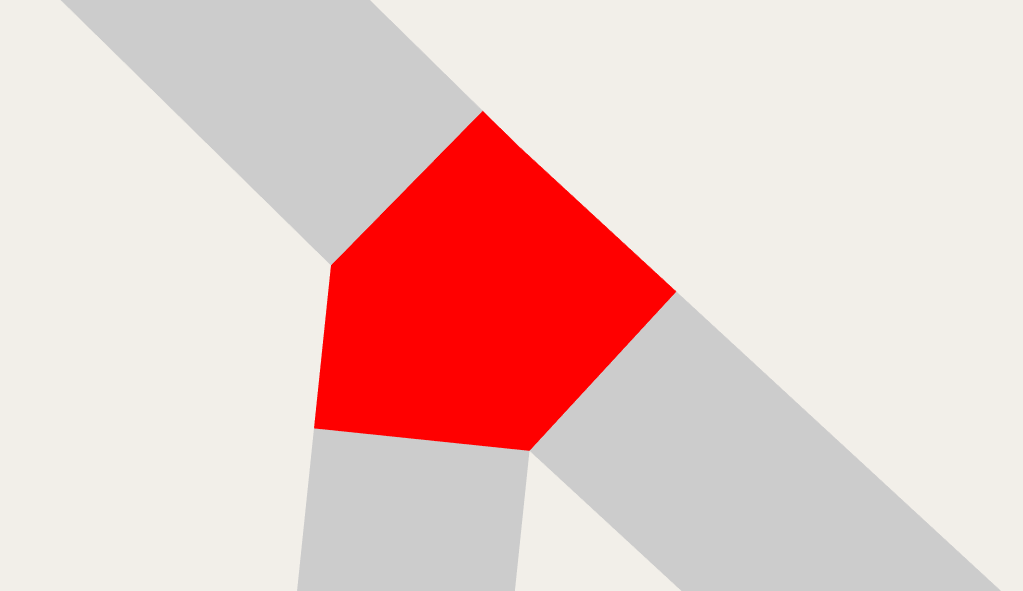
A simplifying assumption, mostly coming from OSM, is that roads can be represented as a center-line and width, and individual lanes can be formed by projecting that center-line left and right. This means when the road changes width in the middle (like for pocket parking or to make room for a turn lane), we have to model that transition as a small "degenerate" intersection, which connects only those two roads.

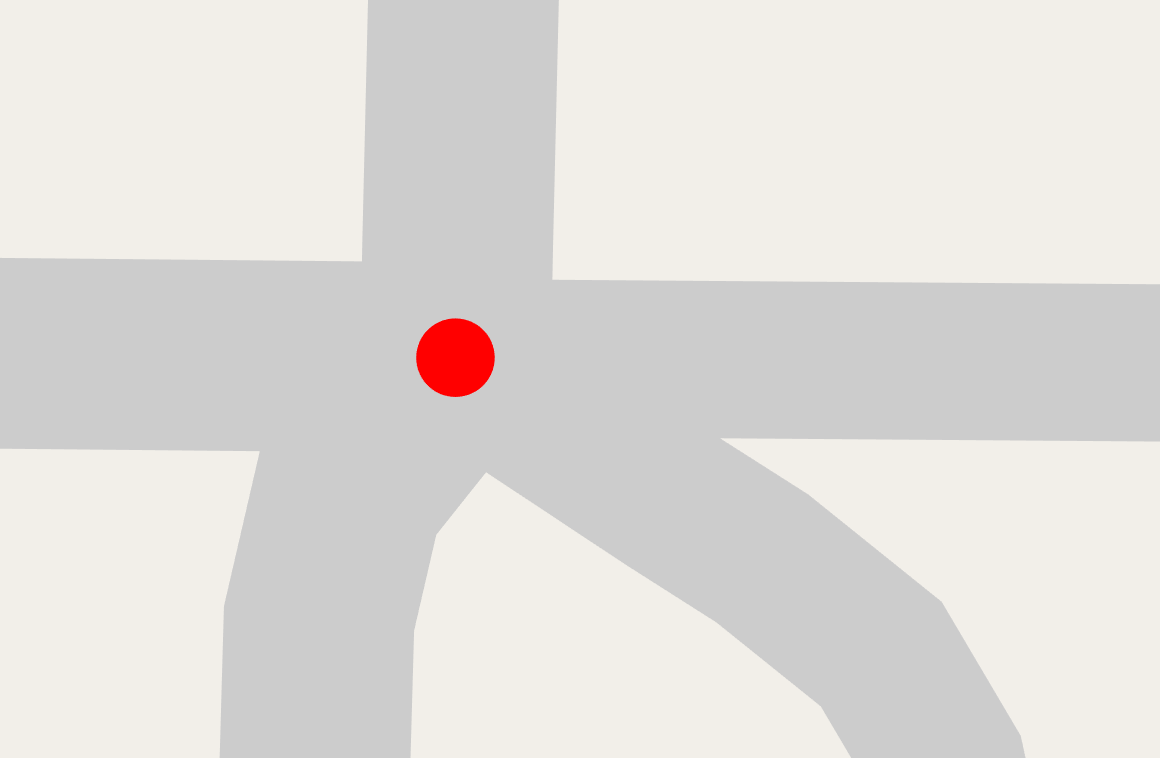
Another assumption taken by A/B Street is that roads hit intersections at a perpendicular angle.
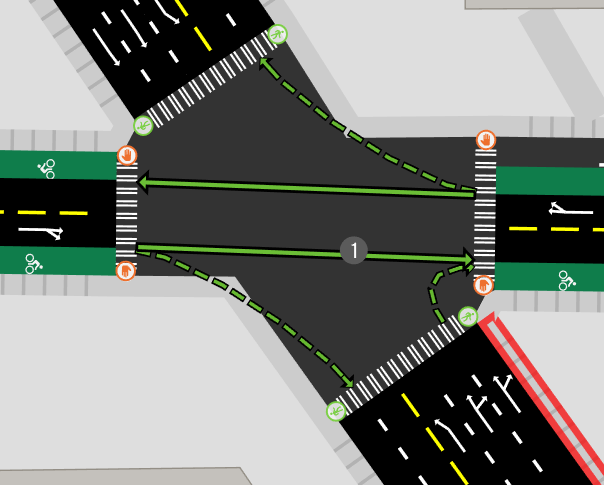
We use this division to determine where vehicles stop, and where a crosswalk exists:
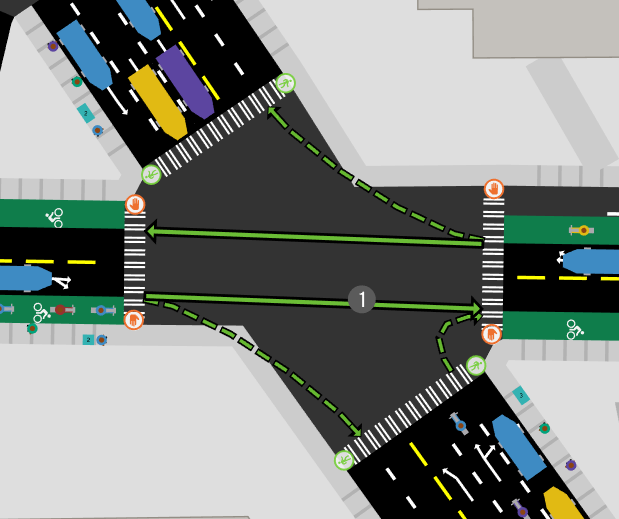
Of course, this assumption isn't always true in reality:

If we allowed roads to hit intersections at non-perpendicular angles, but still insisted that the stop position for each individual lane was perpendicular, it might have a "jagged tooth" look:
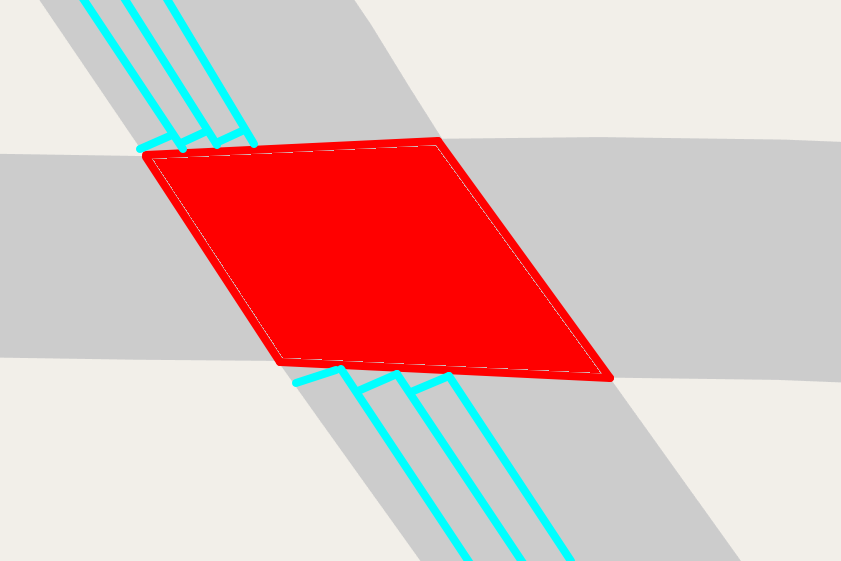
But for the sake of this article, these're the assumptions we're sticking with. Pedestrian islands, slip lanes, gores, and medians are all real-world elements that don't fit nicely in this model.
The main process
We'll now explore the steps to produce geometry for a single intersection and its connected roads. The broad overview:
- Pre-process OSM into road center-lines with attributes, with each road connecting just two intersections.
- Thicken each road
- Trim back the roads based on overlap
- Produce the intersection polygon
Let's pick a particularly illustrative five-way intersection as our example.
Part 1: Thickening the infinitesimal
OSM models roads as a center-line -- supposedly the physical center of the paved area, not the solid or dashed yellow line (at least in the US) separating the two directions of traffic. The schema, and how it gets mapped in practice, is fuzzy when there are more lanes in one direction than the other or when roads join or split up for logical routing, but... let's keep things simple to start.
OSM has a few tags for explicitly mapping road width, but in practice they're not widely used. Instead, we have a whole bunch of tags that describe the lane configuration of the road. A/B Street interprets these and produces an ordered list of lanes from the left side of the road to the right, guessing the direction, width, and type of each lane. See the code here -- it's fairly lengthy, but has some intuitive unit tests. This interpretation of tags is hard in practice because the schema is very confusing, there are multiple ways of mapping the same thing, people make many mistakes in practice, etc.
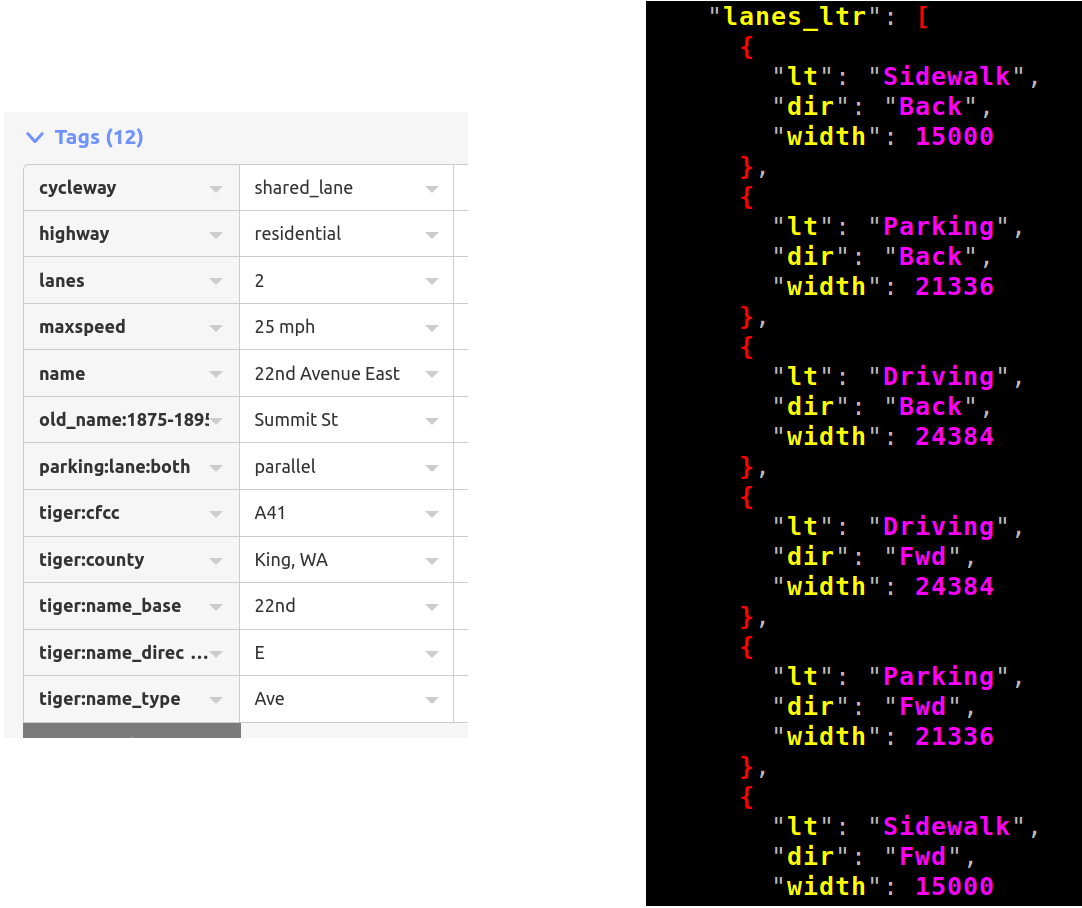
So for each road, we estimate the total width based on the lane tagging. Then we project the center line to the left and right, giving us a thickened polygon for the entire road:
Projecting a polyline
Before we move on, a quick primer on how to take a polyline (an ordered list of points) and project it to the left or right. For a much better explanation, see part 1 and 2 from Rye Terrell's blog. I wouldn't call A/B Street's implementation fantastic, but it's there for reference.
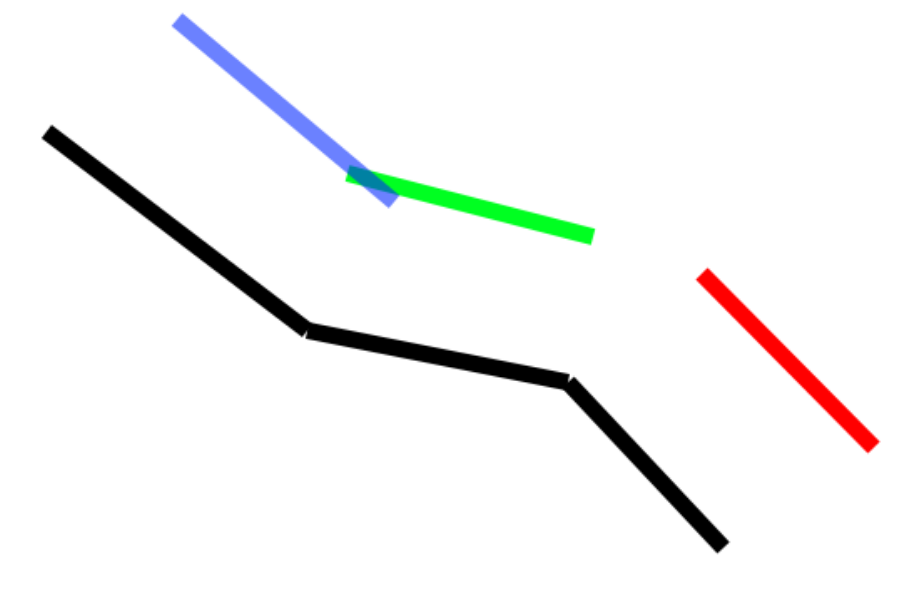
The original polyline is in black. If you can't tell from my quick drawing, it consists of 3 line segments glued together. We want to shift it to the right some distance. We start by taking each line segment and projecting it to the right that distance. That operation is simple -- rotate the line's angle by 90 degrees, then project the line's endpoints that direction. The 3 projected line segments are shown in blue, green, and red.
There are two types of problems we need to fix for the new polyline to be glued together nicely. The blue and the green line segment intersect each other, so we'll trim both segments to that common point:

The green and the red line segments are far apart. Let's imagine they keep extending until they do intersect. If I recall proper terminology, this is a miter join:

And that's it! Easy.
... Except not really. The real world of OSM center-lines has every imaginable edge case. When a road is both thick and sharply angled enough, extending those line segments until they meet works... but the hit might be very far away:
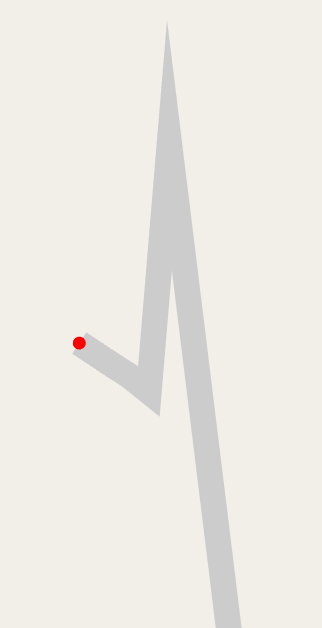
My workaround currently is to hardcode a maximum distance away from the original line endpoints. If our miter cap reaches beyond that, just draw a straight line between the two segments. I think this is known as a bevel join.
Just for fun, let's see what happens when a polyline doubles back on itself in some less-than-realistic ways:
Truly Lovecraftian geometry. I don't think I often see points from OSM totally out of order like this, but it happens sometimes and is immediately obvious.
Part 2: Counting coup
For each road, we've got the original center from OSM and our calculated the left and right side:
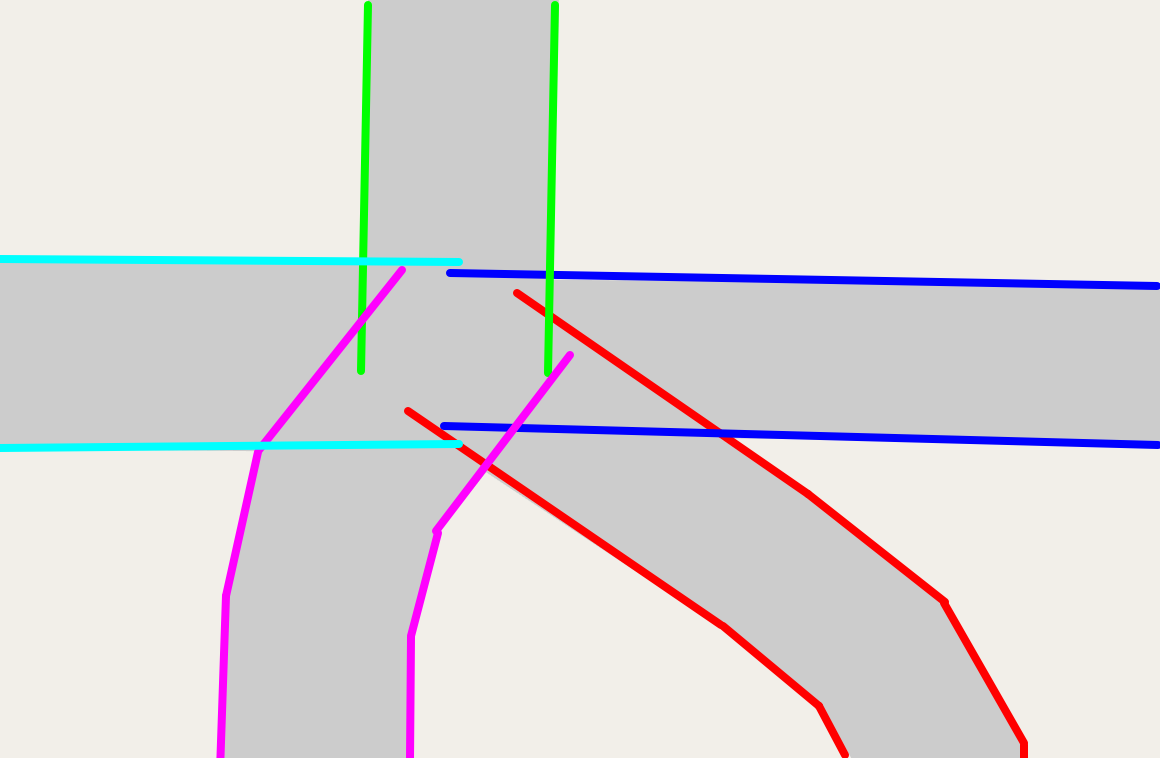
Now the magic happens. You'll notice that many of those polylines collide (For sanity, let's call these "collisions" and not "intersections", since that term is overloaded here!). Let's find every collision point:
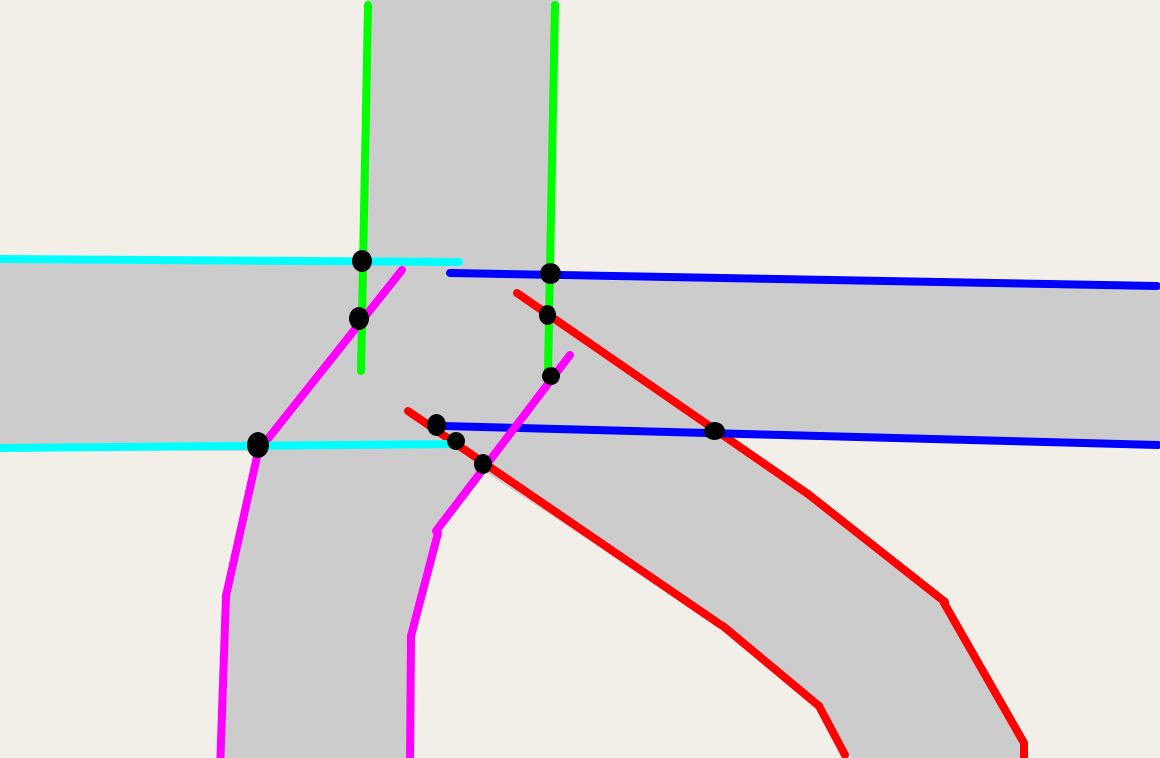
These collisions represent where two thickened roads overlap. So let's use them to "trim back" the roads and avoid overlap. For each collision, we form an infinitely long line perpendicular to the collision and find where it hits the original center-line. We'll trim the road back to at least that point.
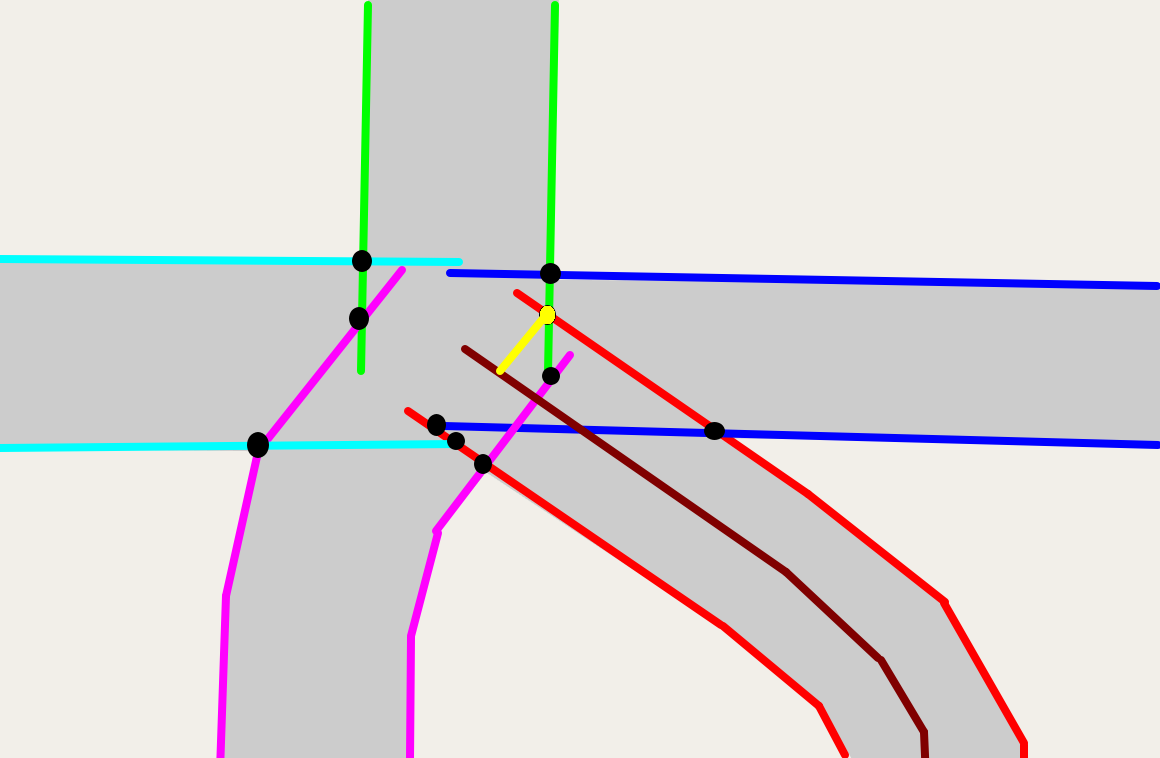
Because we want roads to meet intersections perpendiculously (I'm quite sure that's the proper term), we want the left and right side of a road to line up. There's probably a collision on a road's left and right side, and usually one of them would cause the center-line to be trimmed back more than the other. We'll always trim back as much as possible.
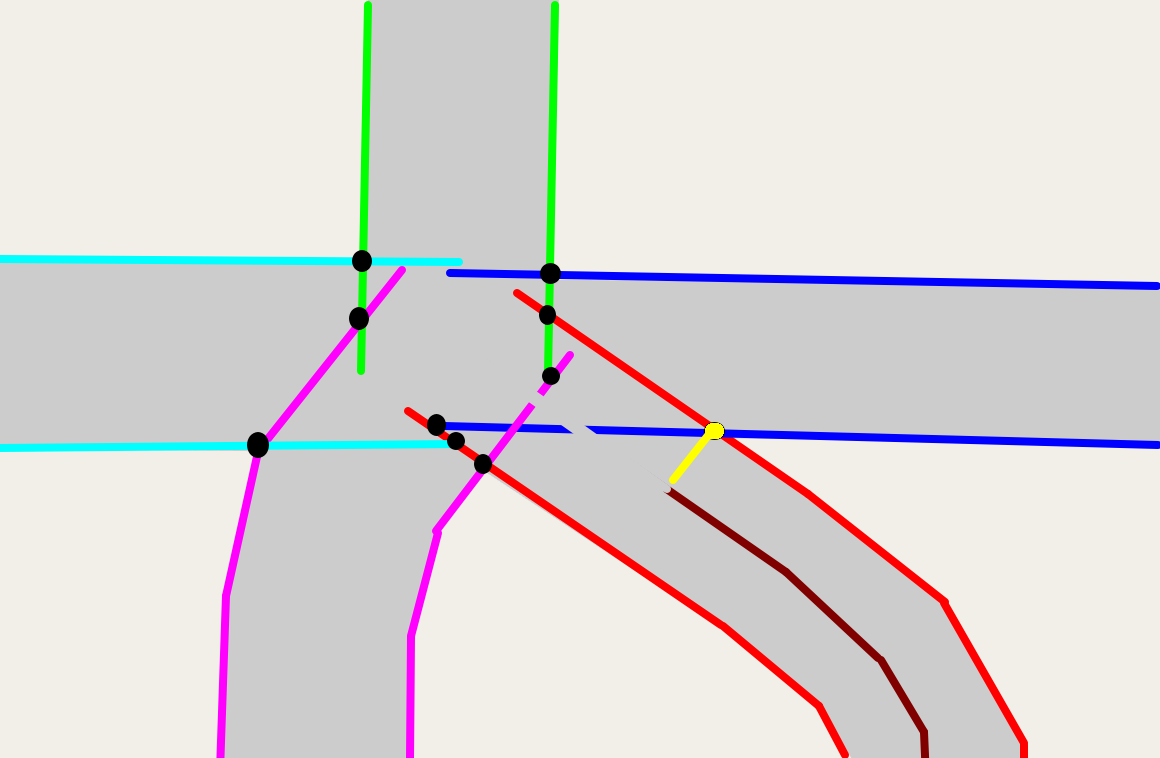
If we repeat this for every collision, eventually we wind up with:
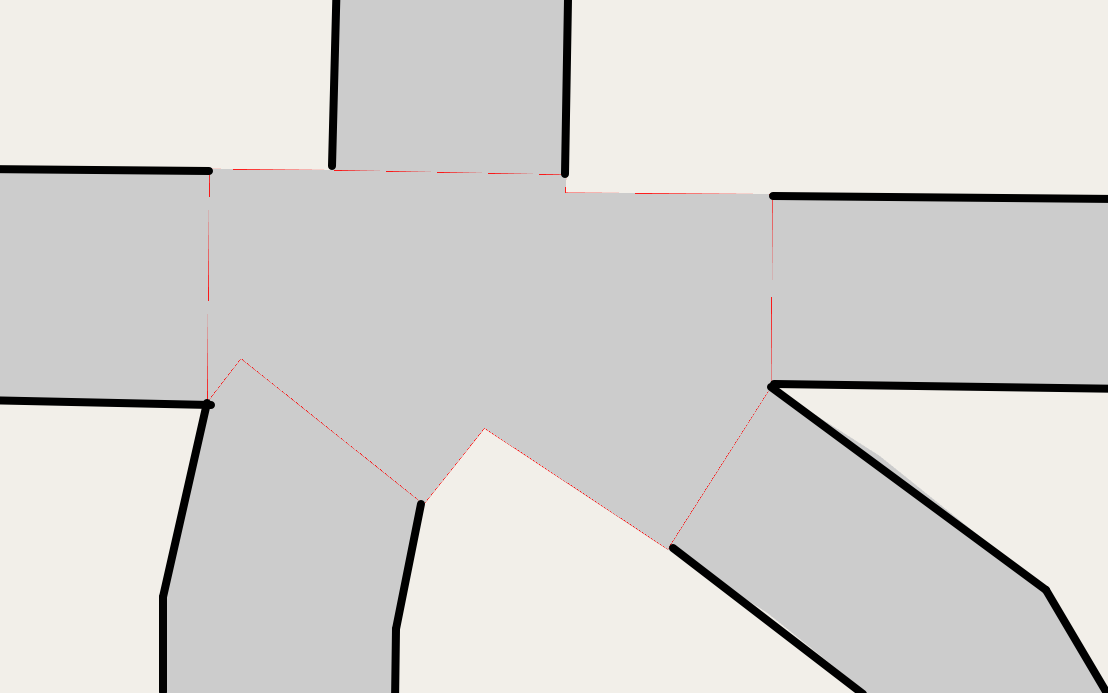
Some questions to consider:
-
Why look for collisions between every pair of left/right lines? Couldn't we just use the "adjacent" pairs?
-
Is it ever possible for the line perpendicular to a collision to NOT hit the original center-line?
(As I'm reviewing my old code and writing this up, these're things I don't remember, worth revisiting.)
Part 3: The clockwise walk
We've now trimmed roads back to avoid overlapping each other. We just need to generate the polygon for the intersection. As a first cut, let's take these trimmed center-lines, calculate the left and right polylines again (since we've changed the center line), and use the endpoints for the shape.
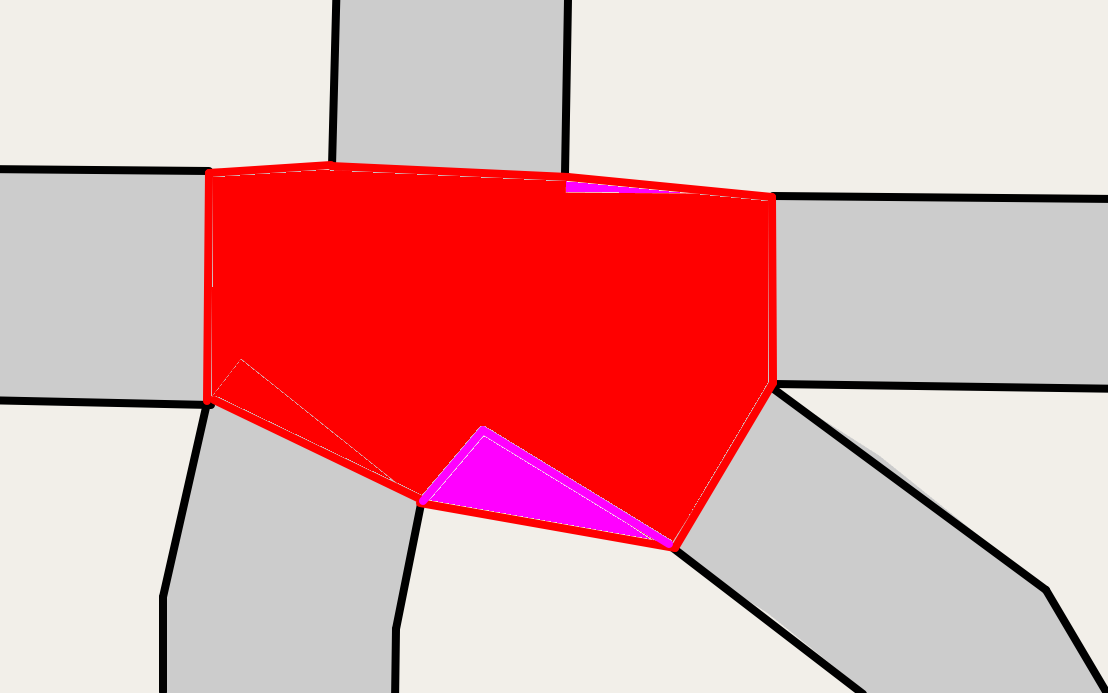
Oops, the polygon covers a bit too much space! Cut red tape, queues, and split ends, but not corners. What if we remember all of the collision points, and use those too?
Much better.
Sorting roads around a center
I snuck a fast one on ya. When we form a polygon from these left/right endpoints and the original collision points, how do we put those points in the correct order? Seemingly innocent question.
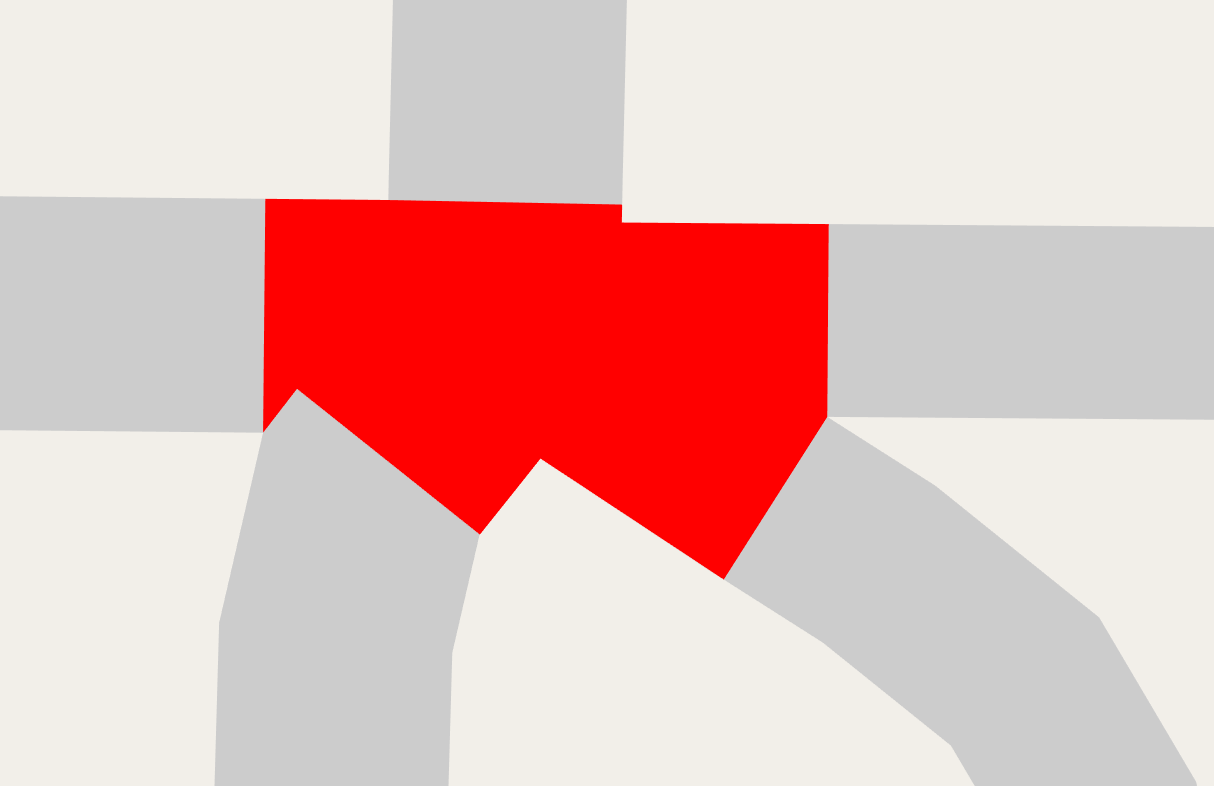
There are a few approaches that work fine for the simple cases. First, from OSM we know the single point where the 5 road center lines meet. After we've calculated the points for the intersection polygon, we can use that single point, calculate the angle to each polygon point, and sort. That works fine.
Foreshadowing: But soon, things won't be so simple.
Interlude: problems so far
That wasn't actually so bad! The results are reasonable in many cases:
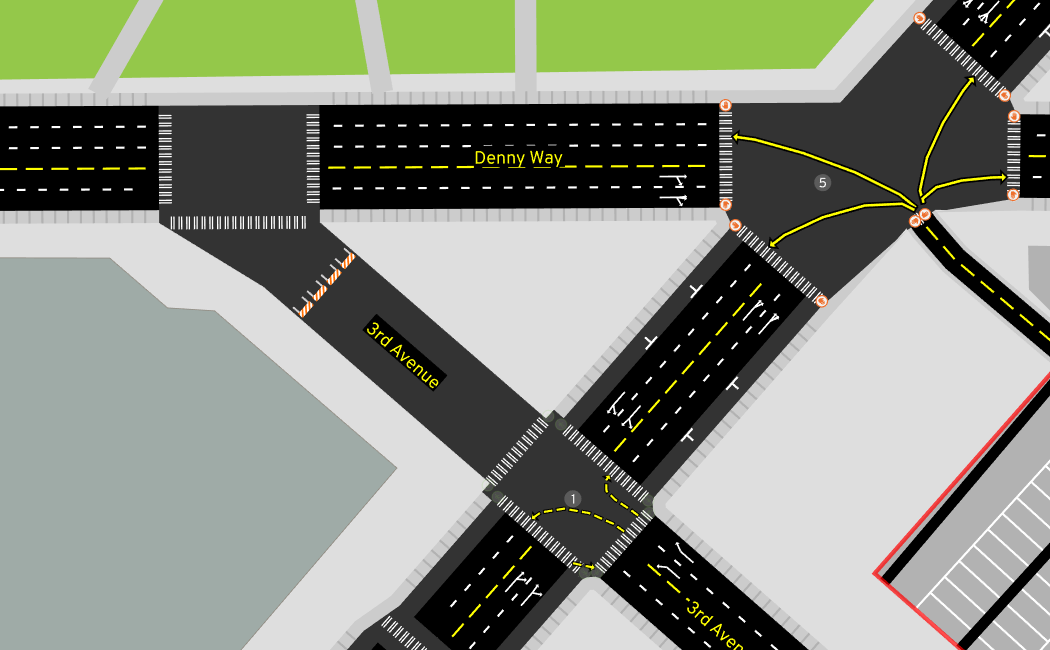
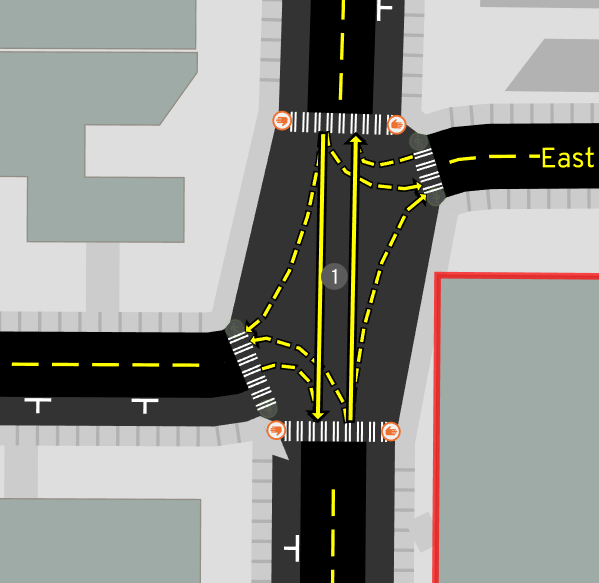
But what kind of things go wrong?
Funky sidewalks
What's going on with the sidewalk in that last example?
Lovecraftian geometry
Sometimes followers of Cthulu edit OSM, I assume.
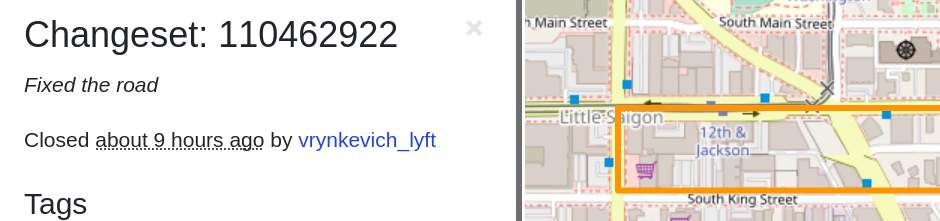
Bad OSM data
Often times, the upstream OSM data is just flat-out wrong. Center lines for divided one-way roads are way too close to each other, so using the number of lanes with a reasonable guess at width produces roads that overlap outside of the intersection. This throws off everything we've done!
Another example is people tagging the lane count incorrectly. A common problem
when splitting a bidirectional road into two one-ways (which is what you're
supposed to do when there's physical separation like a median) is forgetting to
change the lane count.
Here's a recent example,
where sidewalk=both was copied when a bidirectional road was split into
divided one-ways.
An important lesson when trying to write algorithms using OSM data: there's a balance between making your code robust to problems in the data, and trying to fix everything upstream. I attempt a compromise. It's a virtuous cycle -- in trying to use OSM data in this new way, I wind up fixing the data sometimes.
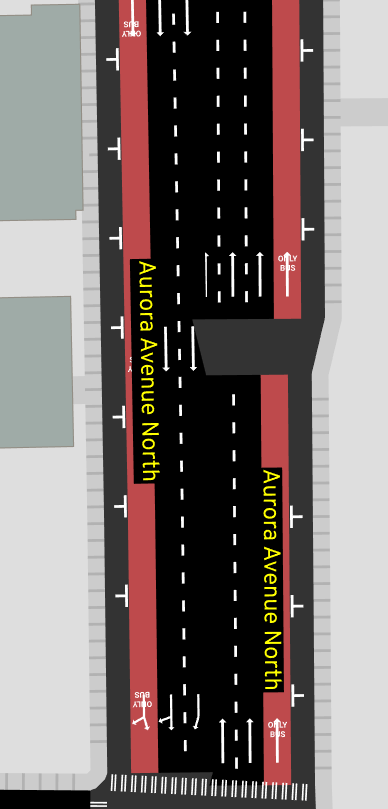
Highway on/off-ramps
When three nearly parallel roads meet, our algorithm is a bit over-eager with the size of the intersection:
This case isn't even a real "intersection" -- a one-way highway has two different off-ramps jut out. At some point, I had some scribbled diagrams in a notebook somewhere from when I worked on this, but it's lost -- luckily the code for this case is pretty simple. This produces much better results here:

OSM has a placement tag that may also be useful here.
Intersection consolidation
The skeptical reader has noticed the suspicious lack of complex intersections so far. Time to dive into that.
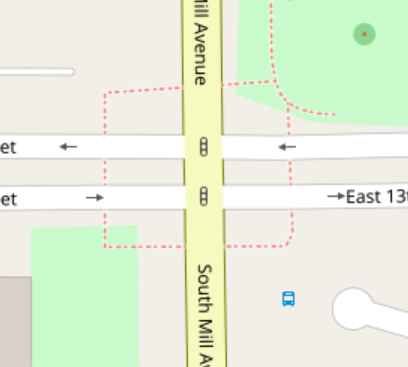
Where short roads conspire
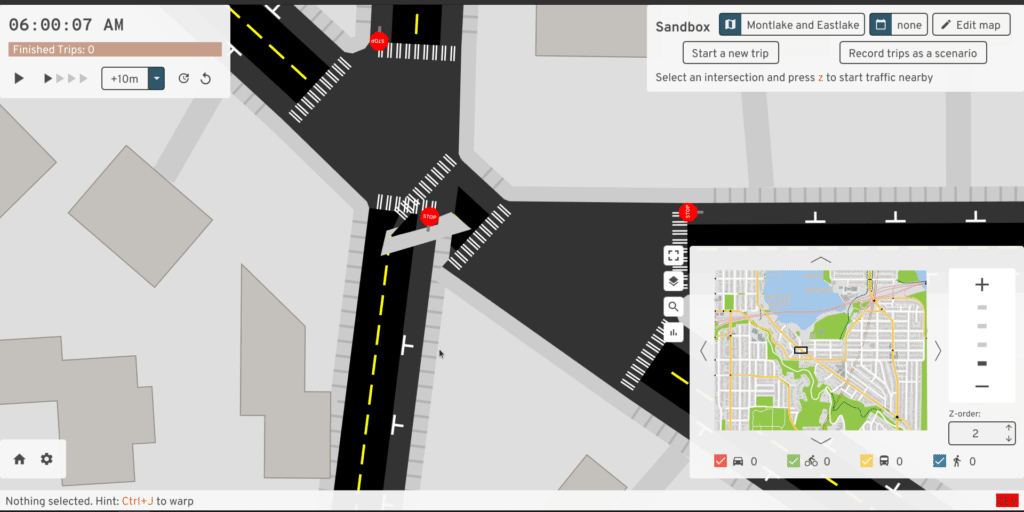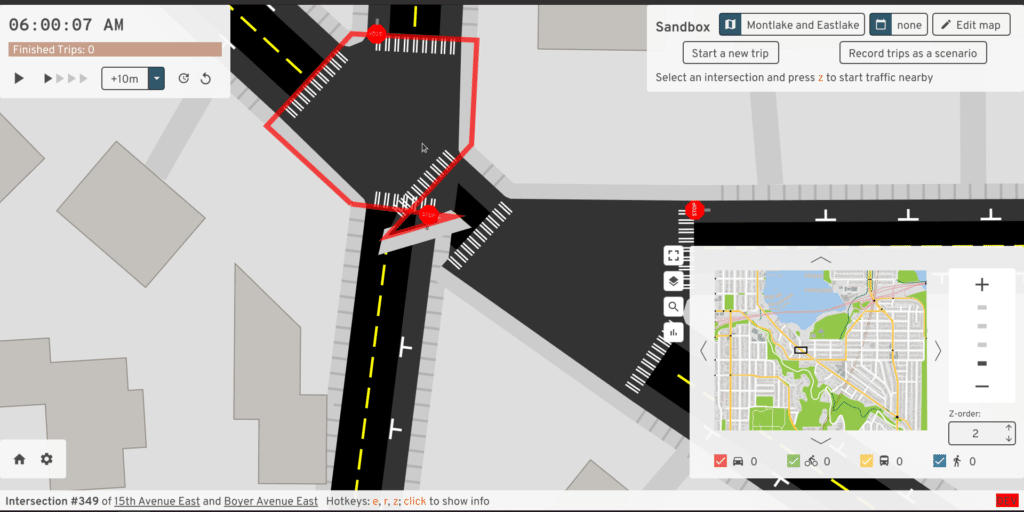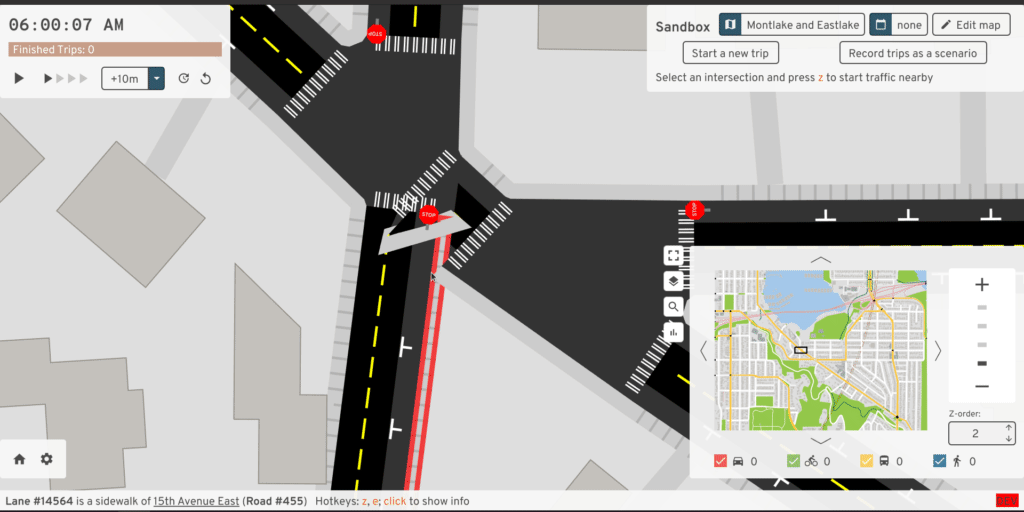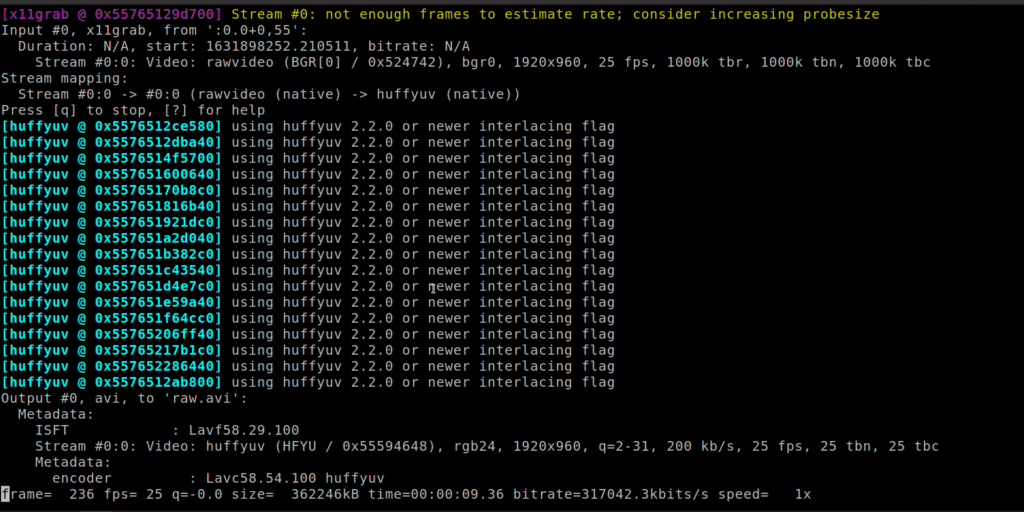
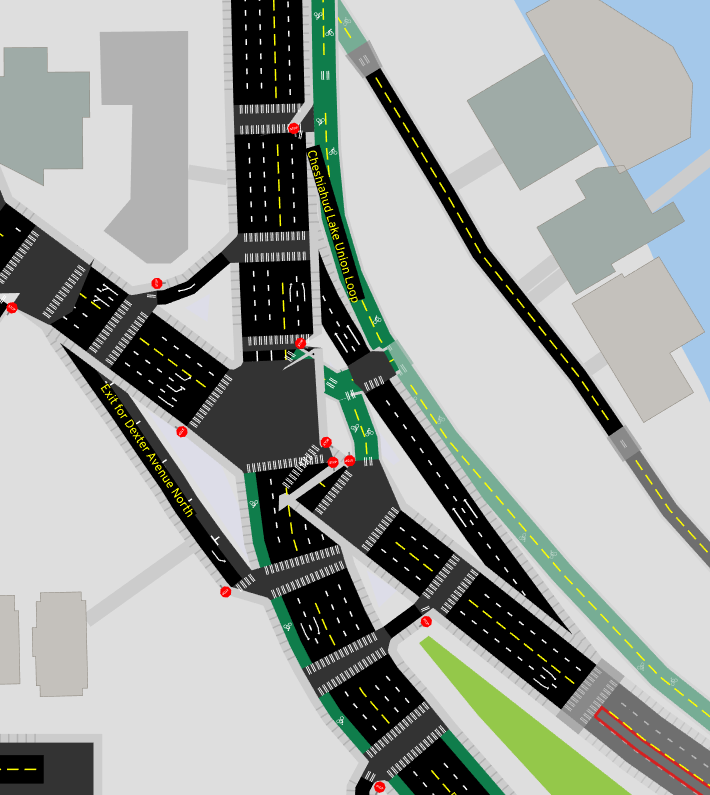
In OSM, roads with opposite directions of traffic separated by any sort of center median -- even if it's just a small raised curb -- are mapped as two parallel one-way roads. These're also called divided highways or dual carriageways. When these intersect, we wind up with lots of short "road segments" and several intersections all clustered together:
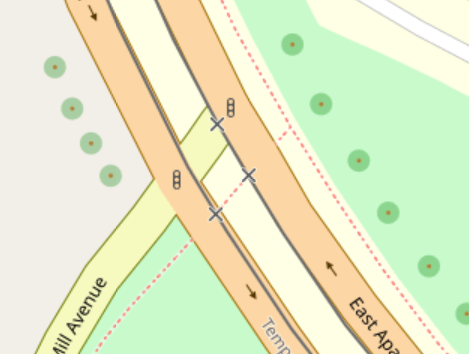
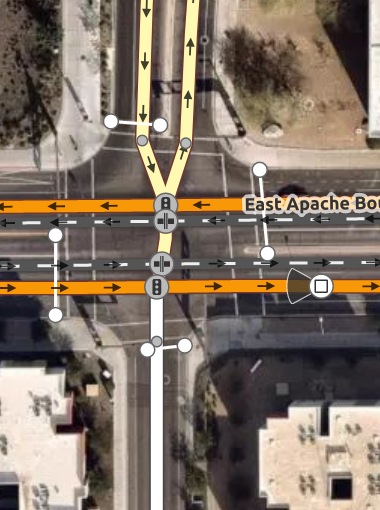
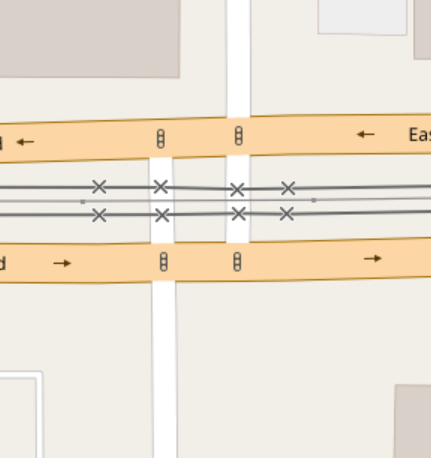
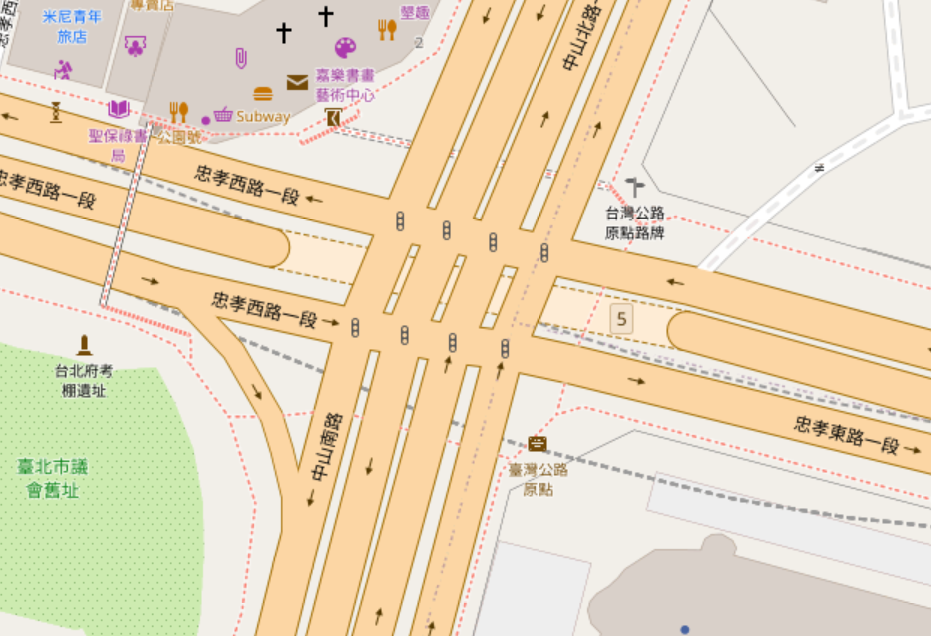
But wait, there's more. How about "dog-leg" intersections, where one road shifts over slightly as it crosses another?
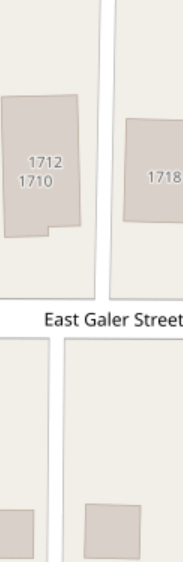
But sometimes something looking like a dog-leg actually isn't -- if vehicles can legitimately stop and queue in the middle of the "intersection", even if it's only one or two of them, then I think that interior "road" deserves to remain separate:
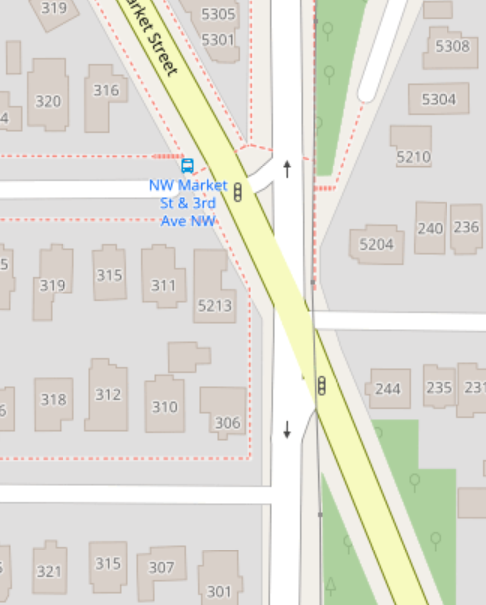
And then there's just the cases where I'm pretty sure civil engineers anticipated me writing this algorithm, and found the most obnoxious angles for roads to meet in order to maximize my pain:

Why we want to do something about it
So hold up, what's the problem? Some areas that people treat as one physical intersection in reality are modelled in OSM as a cluster of intersections, with lots of short "roads" linking them together. It's fine from a graph connectivity and routing perspective. What could go wrong?
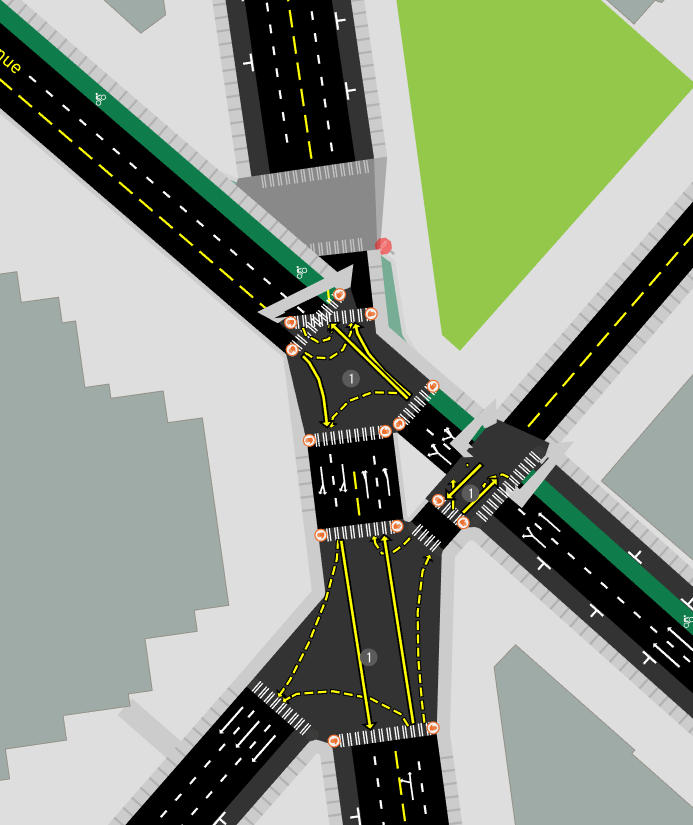
Well for starters, with the algorithm described so far that tries to render the physical shape, it's completely visually incomprehensible:
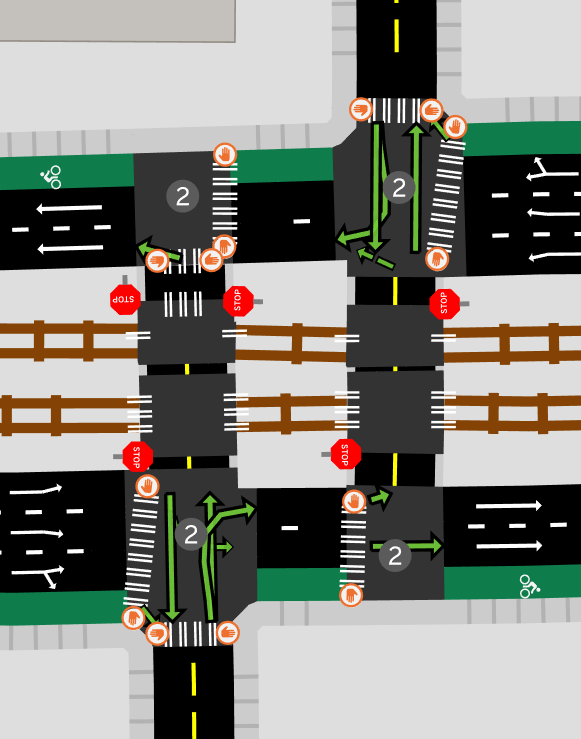
These complicated intersections are often the ones that would be the most interesting to study in A/B Street, but just try modifying lanes in these cases:
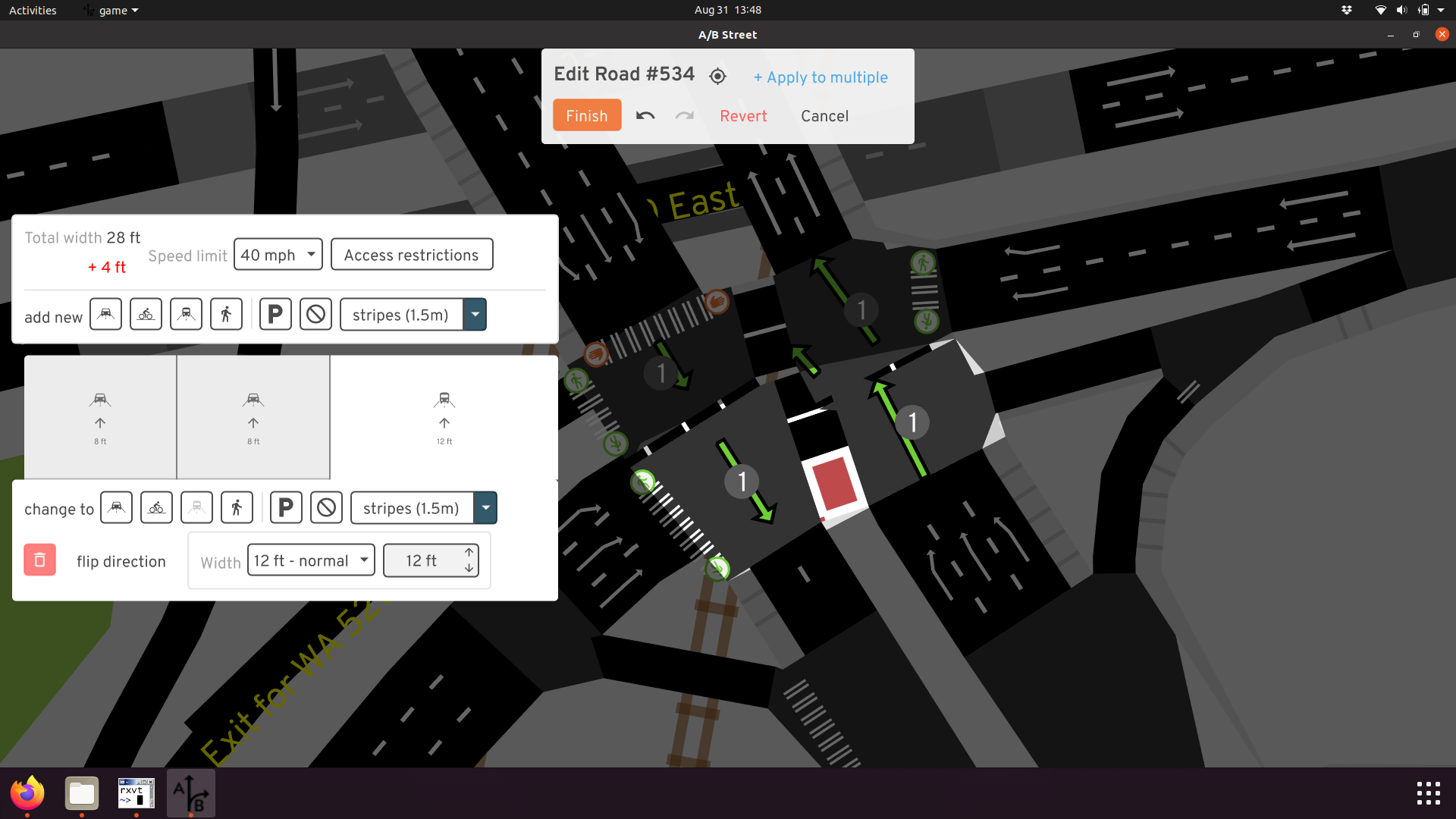
Now throw traffic signals into the mix. A/B Street tries to simulate those, so when we have a cluster of two or four of them super close, now we have to somehow try to synchronize their timing. When somebody wants to edit them, now they have to operate on all of them at once! We even extended the UI to handle that, but it's quite a poor editing experience.
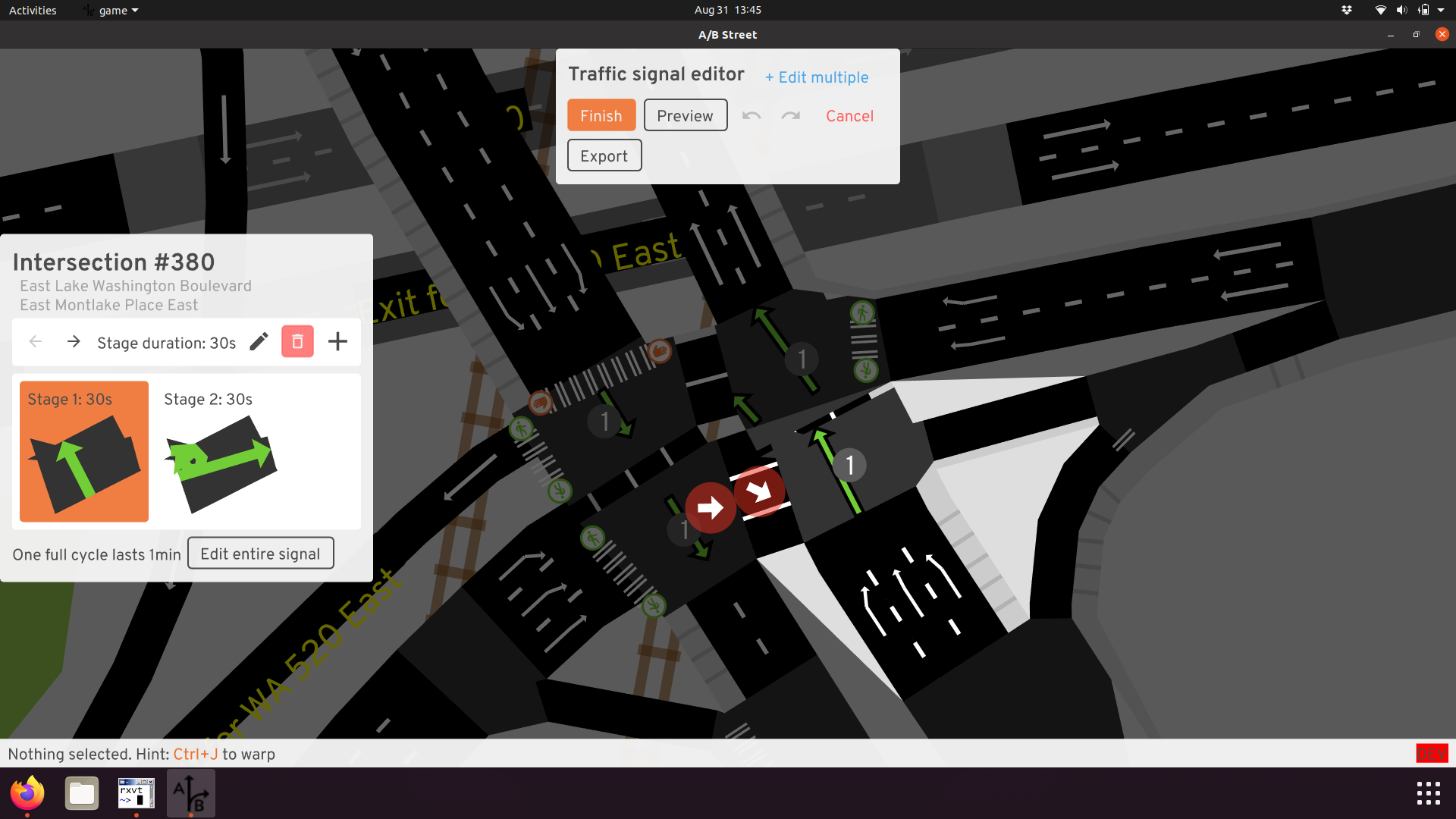
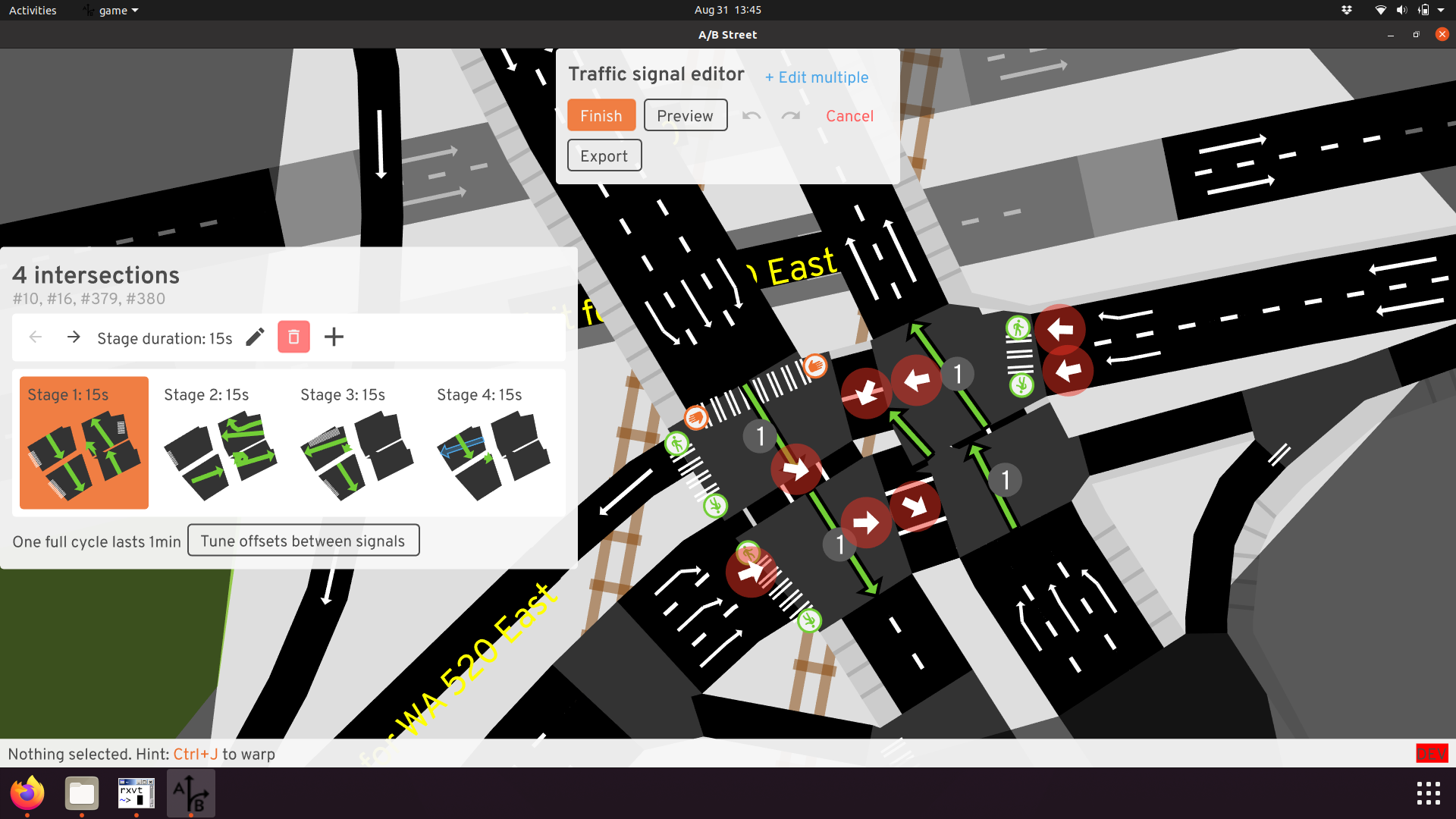
And finally, traffic simulation gets MUCH harder. A/B Street models vehicles as having some length, meaning a vehicle's front can make it through one intersection, but its tail gets stuck there:
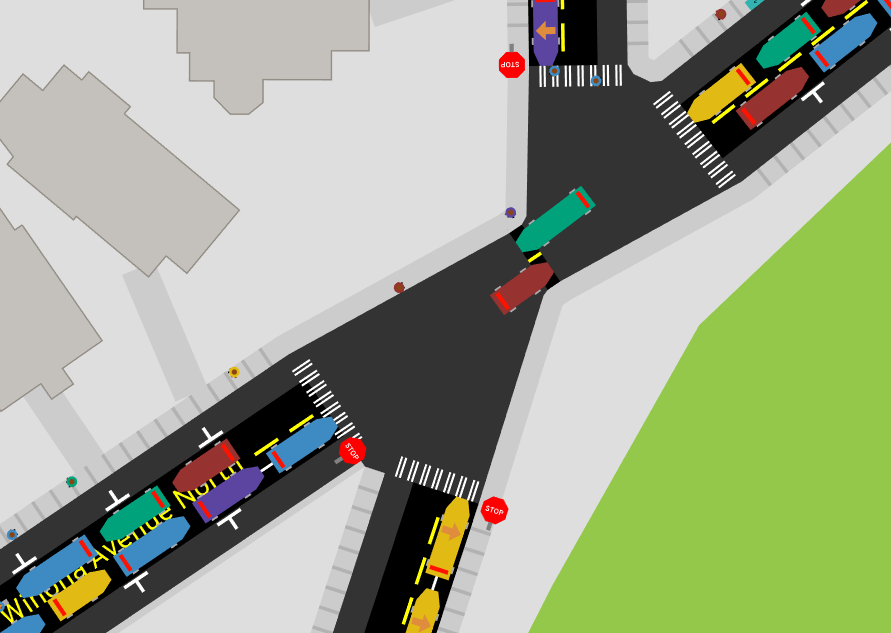
At the simulation layer, vehicles moving through an intersection conflict with each other very coarsely. If a vehicle is partially stuck in the intersection, it prevents other vehicles from starting potentially conflicting turns. So to prevent this problem from happening, the simulation has complicated rules so that vehicles do not "block the box" -- if they enter an intersection, they must be guaranteed to fully exit and clear it, not get stuck somewhere in the middle. These rules blow up in the presence of short roads like this. Lots of effort has gone into workarounds at the simulation layer, but... just fixing the representation in the map model seems much more desirable.
Goal
In reality, many of these clusters of intersections and short roads are actually just one "logical" intersection. If you consider where vehicles stop or where crosswalks are placed, this can make this definition a little bit more clear, but it's somewhat subjective. In A/B Street, we aim to "consolidate" this cluster into just one intersection. Visually coherent geometry, reasoning about a single traffic signal, and preventing vehicles from getting stuck in the cluster are the goals.
Before we dive into the approach to consolidate, let's look at some success stories.
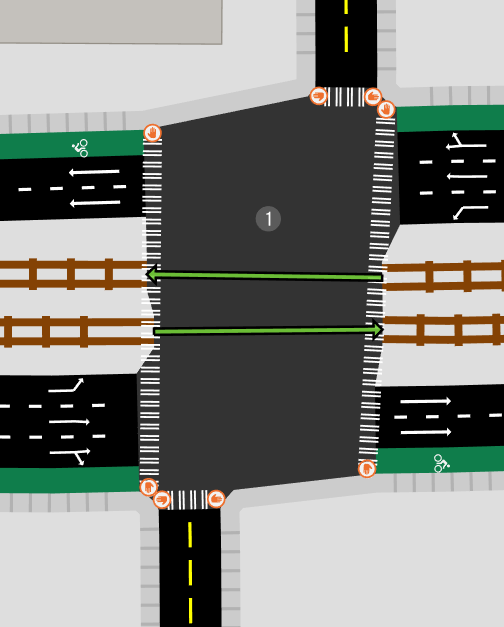
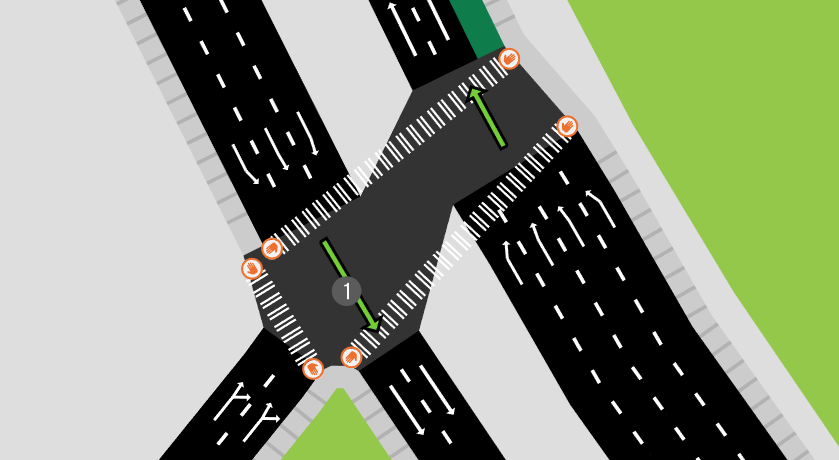
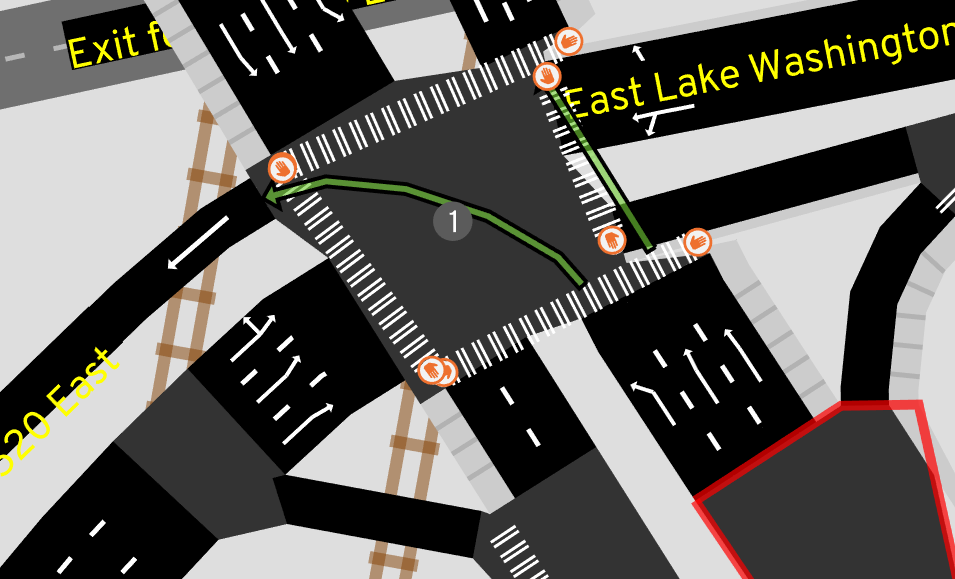
A solution: two passes
For some history getting to this point, check out previous attempts and more before/after examples.
Consolidating a complex intersection happens in a few steps.
- Identify the short roads
- Run the regular algorithm for intersection geometry, and remember how much each road's center line gets trimmed back
- Remove the short road and fix up graph connectivity
- Use the "pre-trimmed" center line to project each surviving road to the left and right
- Assemble those points in order to create the consolidated intersection's polygon
Step 1 and 5 are covered in more detail in below sections.
For step 2, we start with the regular algorithm described so far, applied to each intersection:
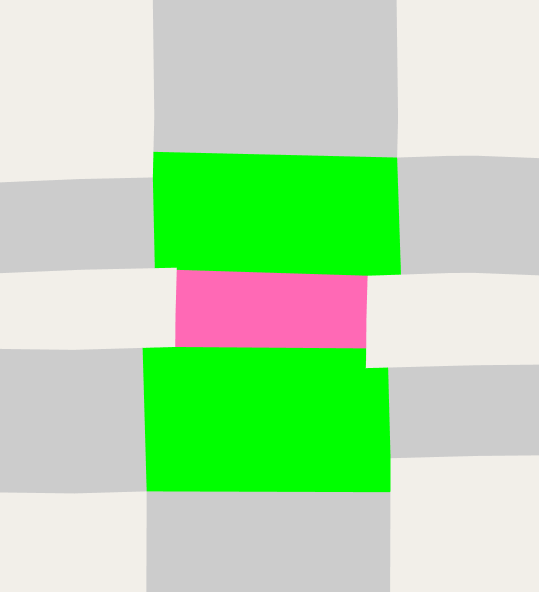
Then we delete the short road. The details of how this is done are particular to A/B Street's intermediate representation of a map model. Graph connectivity and all sorts of turn restrictions must be preserved. But geometrically, it just looks like this:
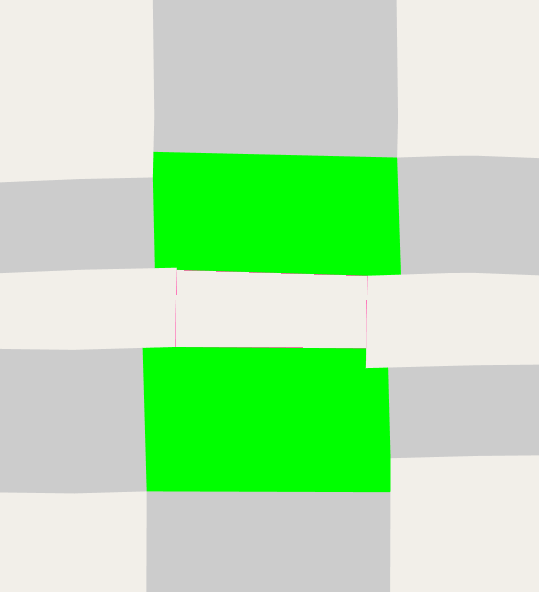
Then we run step 4, finding the left and right side of each surviving road:
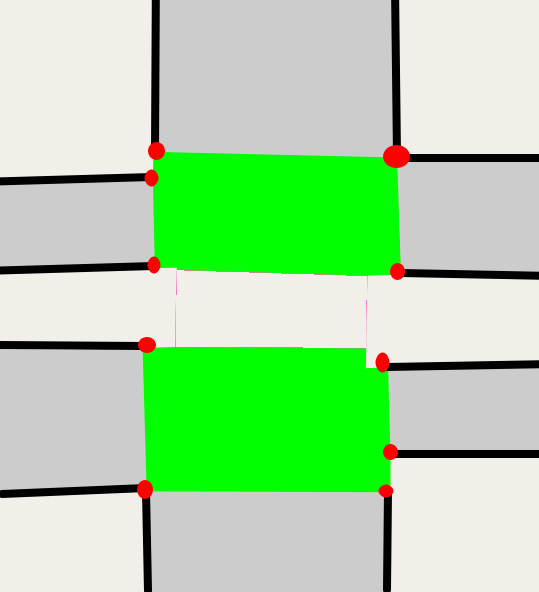
Now if we just use those red dots, we can create the final polygon for this consolidated intersection.
Sorting revisited
To assemble the endpoints into a polygon, we need to know what order they go in. If you recall from an earlier section, we used the original shared point from OSM as the center, and the point farthest away from that shared point to do this:

But now things are less clear -- we have multiple shared points, from before consolidation. As a first pass, maybe we can just average all of the original shared OSM points and call that the "center." And since we've already trimmed back the roads around the complex junction, we can use that point to determine order.
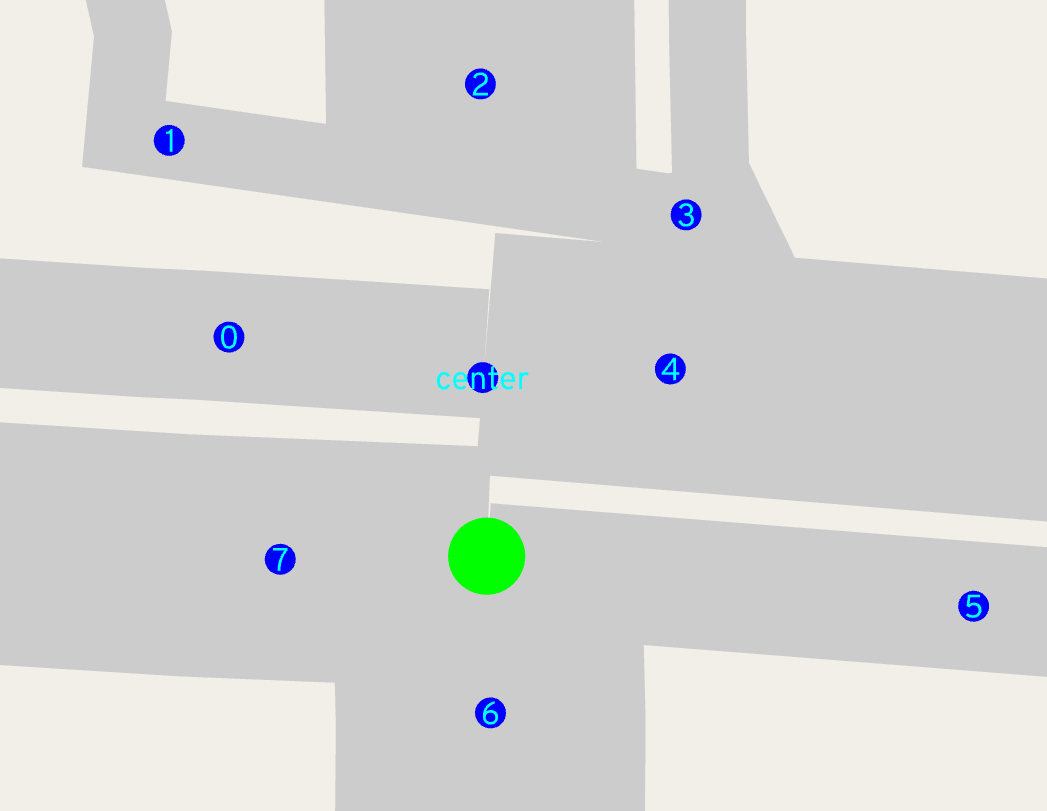
But let's imagine we didn't use that pre-trimmed point, and still used the point farthest from the shared center, like we do for the first pass. Sometimes that can break down!
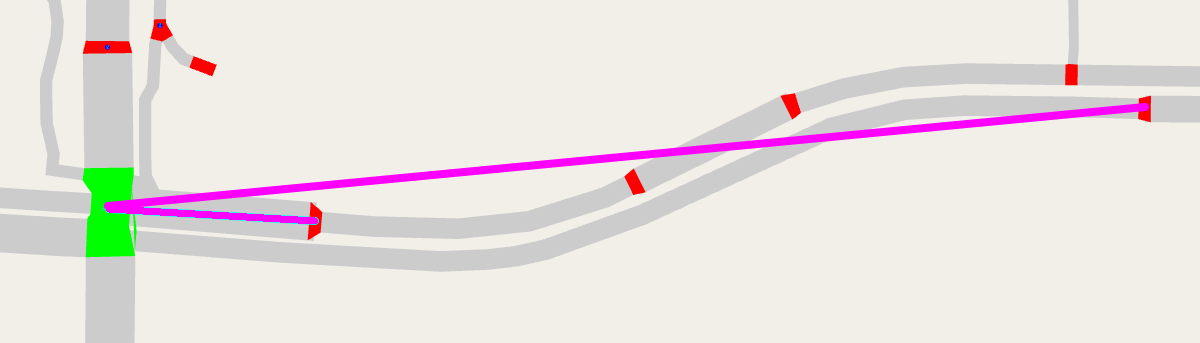
What happens when we get the ordering of roads wrong? The polygon will loop back on itself, looking like a bowtie:
This article has a clever idea to break ties using distance from the center.
Finding the short roads
The algorithm described relies on knowing short roads to merge. Conveniently, there's a proposed OSM tag junction=intersection that describes road segments that're physically located in the interior of intersections. So far, I've been manually tagging this and using it as the trigger to merge a junction. But of course, ideally heuristics would instead discover these cases automatically.
The simplest start is to just define a threshold, like 5 meters, and try to merge any road shorter than that. The road's original length could be used, or -- perhaps more usefully -- we can first generate intersections normally and use the trimmed road length. After merging a short road, perhaps some other ones nearby change their trimmed length, so merging should happen in a fixed-point loop, until no road has changed.
So far, I haven't made good progress with this heuristic. Merging happens in too many places, or in a strange order, and causes assertion failures. Much of the time, this exposes actual bugs, but exposing dozens at a time is hard to handle, so that's why the slower approach of manually opting in a few intersections to merging still remains.
In the spirit of a more gradual rollout of merging code, I've also attempted heuristics just focused on common patterns of complex junctions with 2 or 4 pieces, resulting from one or two divided highways crossing. Sometimes just looking for two or four traffic signal nodes close to each other reveals really complex situations that break:

Phantom collisions
There's a particularly insidious edge case not handled yet:
How could we handle this? Is it necessary to consider collisions between roads one or two hops away in the graph, in case they might be thick enough to interfere?
Conclusion
Given how much time I've sunk into automatically generating decent geometry from an OSM schema absolutely not meant for this, I hope you don't fault me for wanting to try some radically different ideas. There've been some OSM proposals over the years to just explicitly draw roads and intersections as areas -- the street area and area:highway pages describe these ideas the best. These proposals don't seem to have caught on, but I think they're worth an attempt.
I've also toyed around with designing a schema to map roads and intersections from scratch, but that's an article to write on a rainier day...
Appendices
Related work
I've found a few other active projects aiming to render details about lanes:
- https://github.com/enzet/map-machine
- http://blog.imagico.de/navigating-the-maze-part-1/ (and don't miss part 2!)
- https://github.com/BjornRasmussen/Lanes (there are some nice demos in the OSMUS Slack somewhere)
- micro-map of Neukölln in Berlin, see this blog for an introduction
Tricks and tooling
Iterating quickly on these algorithms and preventing regressions are often at odds. These are some parts of my development workflow that help balance a bit.
First, how do you automatically test this? Expressing properties about the output -- like no road and intersection polygons should overlap -- would be a start, but it's a tough standard to reach. It's easy for a human to subjectively judge output and spot regressions. So, screenshot diff-testing it is! For a select few maps, I take a bunch of screenshots covering the whole map and store them as "golden-files." After importing new OSM data or changing the code, I take more screenshots, then automatically compare them with imagemagick's compare tool and manually inspect any differences.
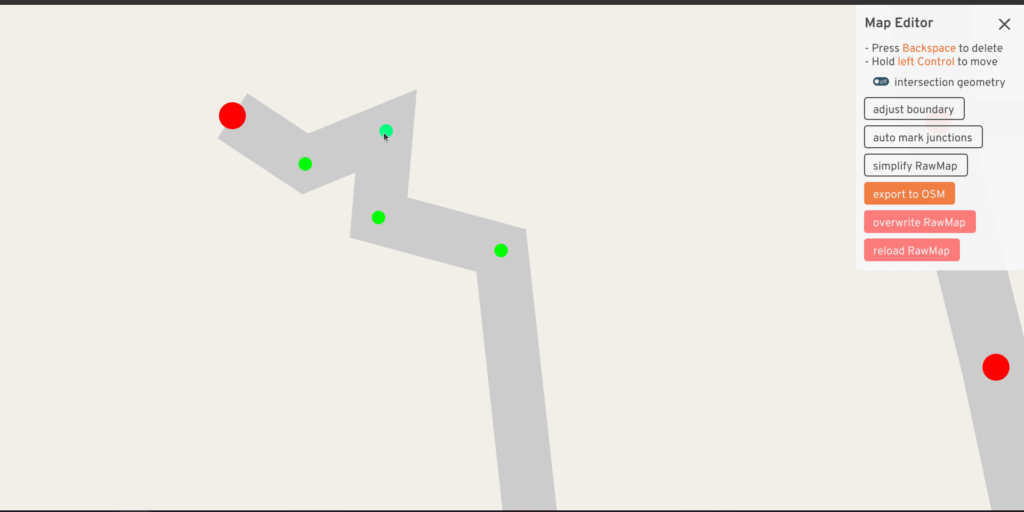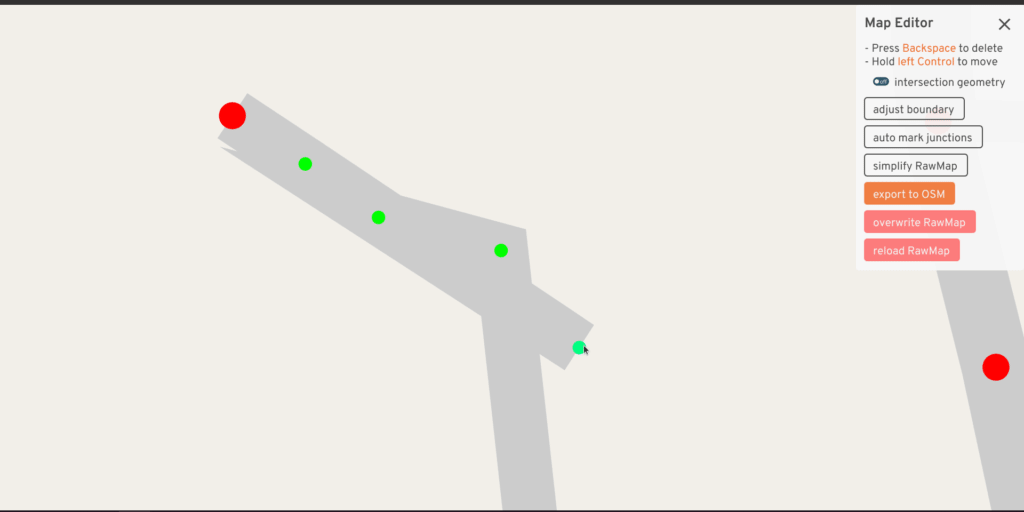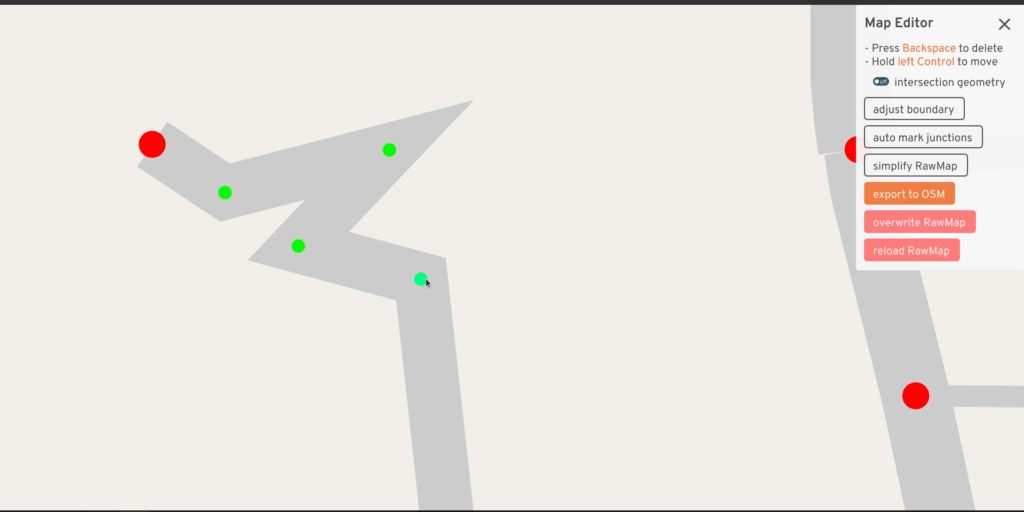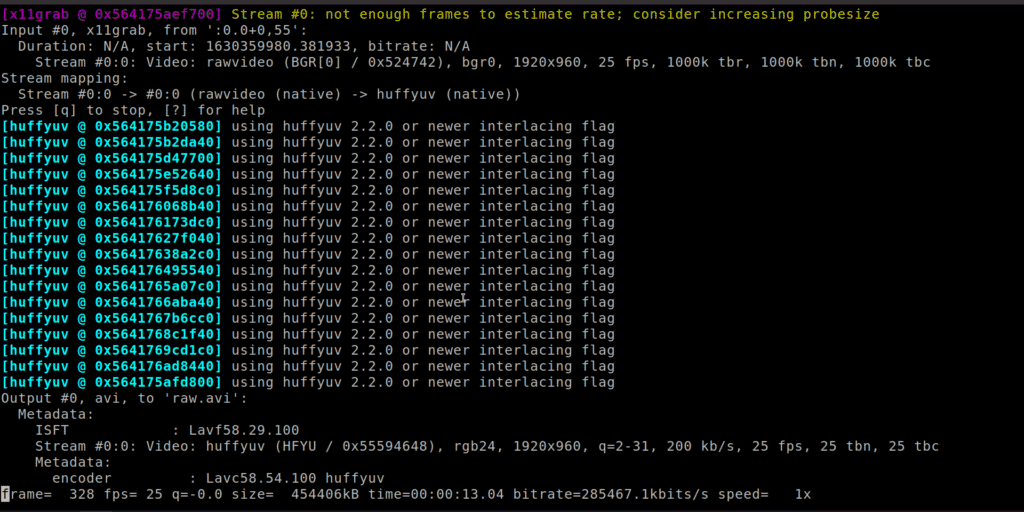
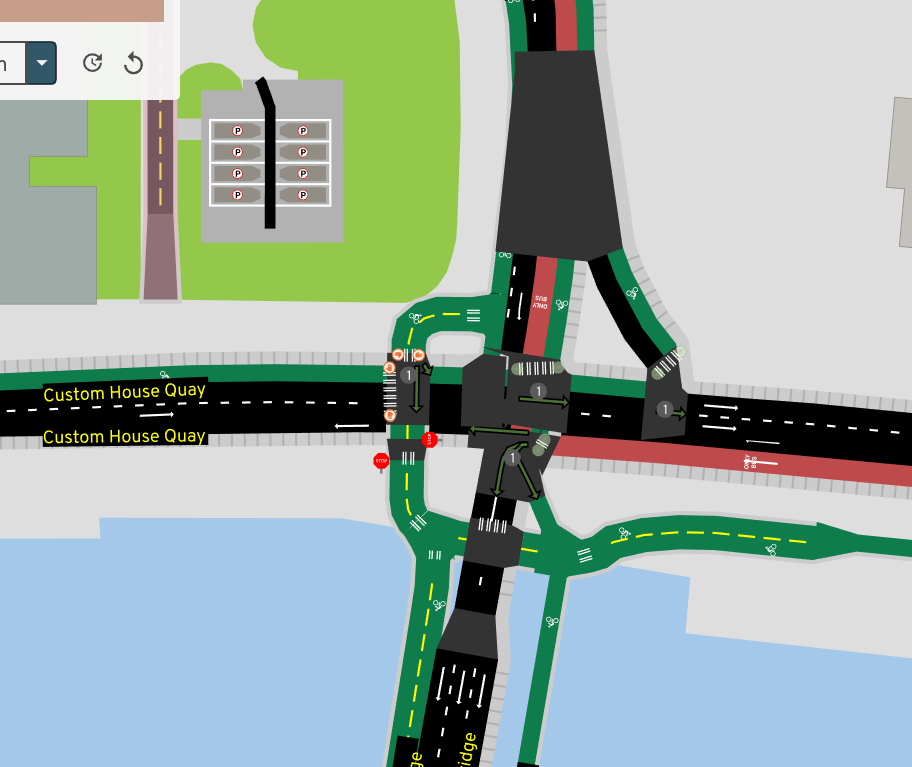
The RawMap editor serves as an interactive tool for quickly adjusting the input -- what if this road center-line curved less sharply, what if the width implied by tags was a little different, what if this road was marked for merging? But at the same time, just previewing the intersection geometry doesn't reveal all problems -- sometimes the turns generated at a consolidated intersection are wrong, or the traffic signal heuristic turns out poorly. The full A/B Street UI already has tools to explore these things. So this UI also has a mode to load a second map and quickly flip between the two:
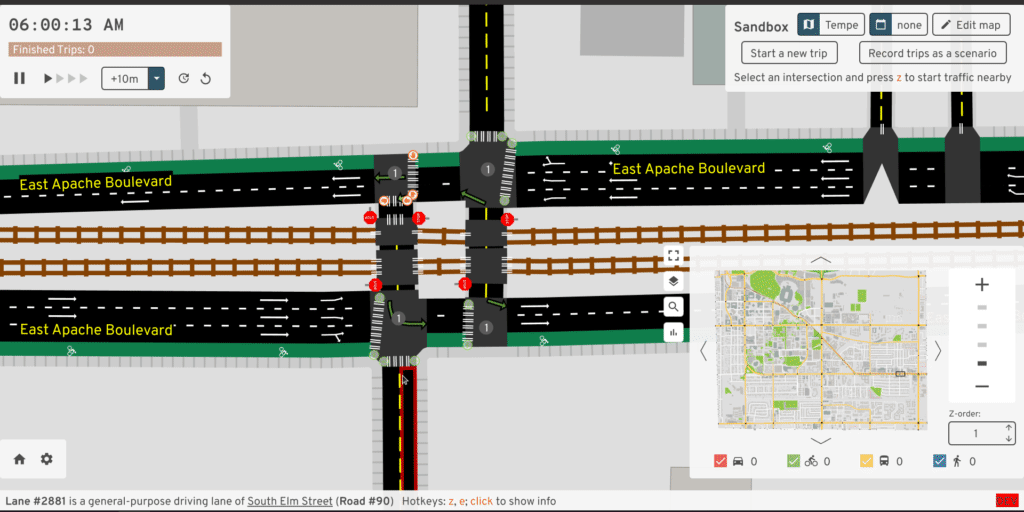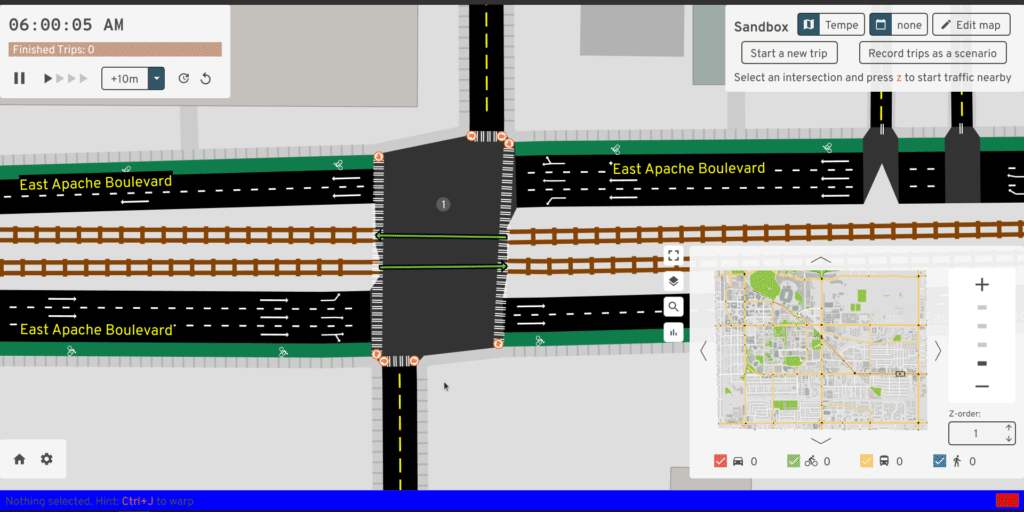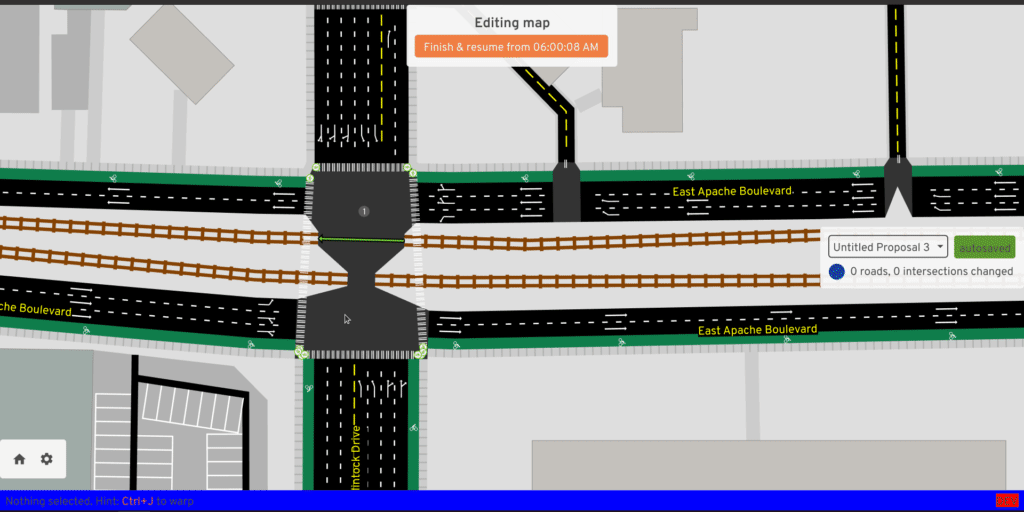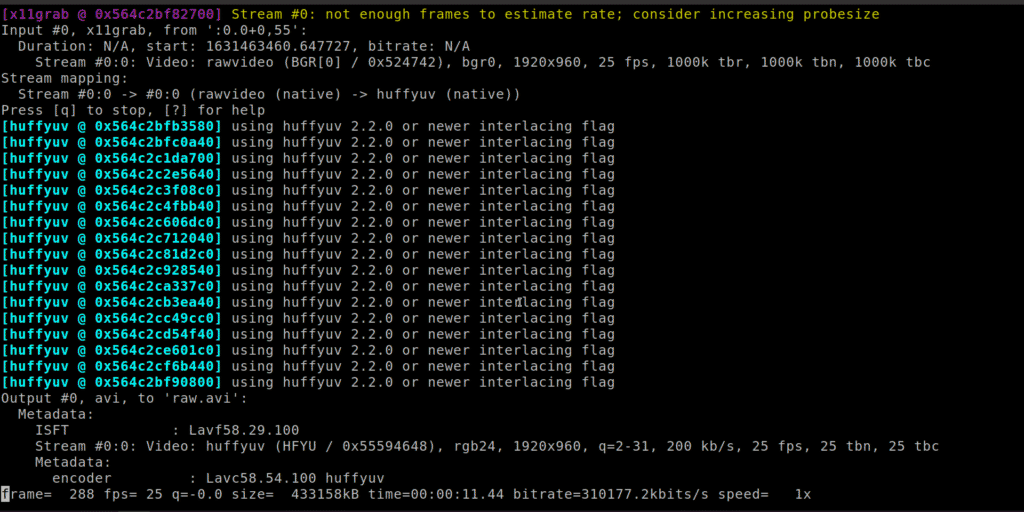
Something I've always wanted is an interactive debugger -- the ability to step through the code, print things, and more importantly, dump some kind of extra output files to visualize intermediate shifted polylines or something. I've never figured out an IDE setup for this, but it'd be very worthwhile.
Hall of Lovecraftian horrors
Here's my list of stress test cases. Avert your eyes...

A radically simpler approach?
I think many people's first instinct to solve the problem of forming an intersection polygon from thickened roads is to use boolean operations. Just find the intersection between all of the road polygons. Or maybe, find the intersection between any pair of road polygons, then union all of those pieces.
Early on, I tried some variations of this. One difficulty was a lack of a robust boolean geometry library in Rust, but if bindings to a native GEOS library were acceptable, maybe this was possible. But also, this simple idea doesn't work for three-way intersections:
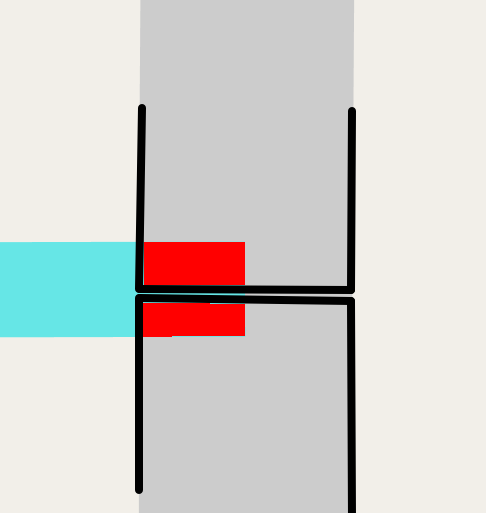
The two vertical road pieces don't even intersect at all, except right at their boundary. We'd need to special-case that, at least.
Other data sources
I've come across a few cities that seem to have a vector dataset describing road polygons or curbs. I haven't tried working with any of these before, but it would be a useful exercise to start with one of these as the base, and snap OSM road segments to this to get metadata about lanes and connectivity, but not geometry.
- Seattle Streets Illustrated
includes some kind of CAD basemap that looks amazingly realistic
- From some old emails with King County GIS, this is based on an impervious surface layer with a license preventing it from being released as public data
- Actually, https://data.seattle.gov/dataset/Pavement-Edge-zip/gy82-cq84 appears to be the curbs for Seattle! Possibly the data is from 1999, updated maybe in 2011.
- https://distanciamiento.inspide.com appears to have detailed sidewalk polygons for Madrid
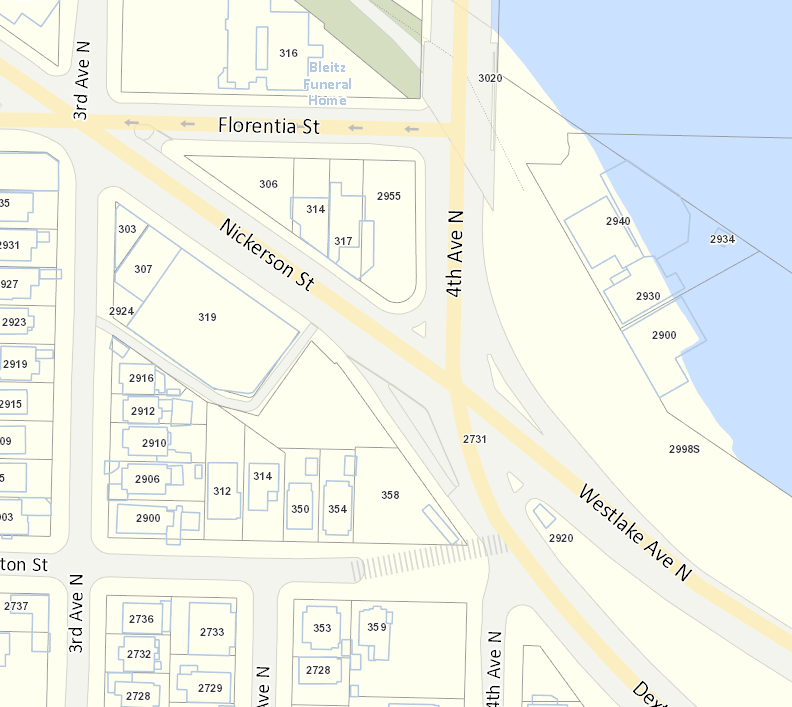
These vector datasets feel like some sort of holy grail, but all of the work described in this article is still useful, because:
- Not every city has this kind of public data
- If road edits need to legitimately widen or shrink a road, it's not obvious how to modify these curbs. But then again, just rechannelizing lanes, subject to the area that's already been paved, is kind of the main type of edit in A/B Street...